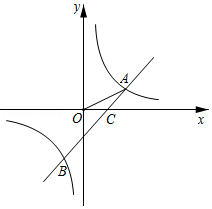
如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.
一次函数 y= ax+ b和反比例函数 y= 在同一直角坐标系中的大致图象是( )
| A. |
|
| B. |
|
| C. |
|
| D. |
|
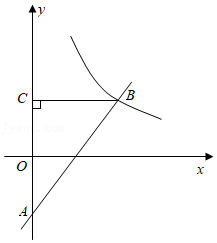
如图,一次函数 的图象与反比例函数 的图象相交于 和 两点.
(1)求反比例函数的解析式;
(2)求点 的坐标.

已知抛物线 y= x 2+2 x+ k+1与 x轴有两个不同的交点,则一次函数 y= kx﹣ k与反比例函数 y=  在同一坐标系内的大致图象是( )
在同一坐标系内的大致图象是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
在平面直角坐标系中,分别过点 , 作 轴的垂线 和 ,探究直线 ,直线 与双曲线 的关系,下列结论中错误的是
A.两直线中总有一条与双曲线相交
B.当 时,两直线与双曲线的交点到原点的距离相等
C.当 时,两直线与双曲线的交点在 轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
如图,已知一次函数 y=﹣ x+ b与反比例函数 y= ( k≠0)的图象相交于点 P,则关于 x的方程﹣ x+ b= 的解是 .

如图,一次函数 的图象与反比例函数 的图象相交于点 、 两点.
(1)求一次函数表达式;
(2)求 的面积.

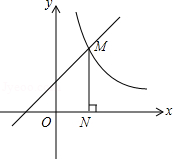
如图,一次函数y1=x+1的图象与反比例函数 的图象交于点M,作 轴,N为垂足,且 。
(1)在第一象限内,当x取何值时, ?(根据图象直接写出结果)
(2)求反比例函数的表达式.
如图,一次函数 y=﹣ x+1的图象与 x轴、 y轴分别交于点 A、 B,以线段 AB为边在第一象限作等边△ ABC.
(1)若点 C在反比例函数 y= 的图象上,求该反比例函数的解析式;
(2)点 P(2 , m)在第一象限,过点 P作 x轴的垂线,垂足为 D,当△ PAD与△ OAB相似时, P点是否在(1)中反比例函数图象上?如果在,求出 P点坐标;如果不在,请加以说明.

已知反比例函数 y= ( k为常数).
(1)若点 P 1( , y 1)和点 P 2(﹣ , y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较 y 1和 y 2的大小;
(2)设点 P( m, n)( m>0)是其图象上的一点,过点 P作 PM⊥ x轴于点 M.若tan∠ POM=2, PO= ( O为坐标原点),求 k的值,并直接写出不等式 kx+ >0的解集.
如图,直线 与双曲线 相交于 、B两点,在y轴上找一点P,当 的值最小时,点P的坐标为 .

在直角坐标系中,设函数 是常数, , 与函数 是常数, 的图象交于点 ,点 关于 轴的对称点为点 .
(1)若点 的坐标为 ,
①求 , 的值;
②当 时,写出 的取值范围;
(2)若点 在函数 是常数, 的图象上,求 的值.

如图,一次函数 的图象与反比例函数 的图象交于点 、 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式 的解集.