初中数学反比例函数的性质试题

如图，一次函数 $y=k_{1}x+b(k_1\ne 0)$ 与反比例函数 $y=\frac{k_2}{x}(k_2\ne 0)$ 的图象交于点 $A(2,3)$ ， $B(n,-1)$ ．

（1）求反比例函数和一次函数的解析式；

（2）判断点 $P(-2,1)$ 是否在一次函数 $y=k_{1}x+b$ 的图象上，并说明理由；

（3）写出不等式 $k_{1}x+b⩾\frac{k_2}{x}$ 的解集．

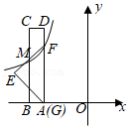
如图，将一把矩形直尺 $\mathit{ABCD}$和一块等腰直角三角板 $\mathit{EFG}$摆放在平面直角坐标系中， $\mathit{AB}$在 $x$轴上，点 $G$与点 $A$重合，点 $F$在 $\mathit{AD}$上， $\mathit{EF}$交 $\mathit{BC}$于点 $M$，反比例函数 $y=\frac{k}{x}(x<0)$的图象恰好经过点 $F$， $M$，若直尺的宽 $\mathit{CD}=1$，三角板的斜边 $\mathit{FG}=4$，则 $k=$　　．

在平面直角坐标系中，对于不在坐标轴上的任意一点 $A(x,y)$ ，我们把点 $B(\frac{1}{x}$ ， $\frac{1}{y})$ 称为点 $A$ 的"倒数点"．如图，矩形 $\mathit{OCDE}$ 的顶点 $C$ 为 $(3,0)$ ，顶点 $E$ 在 $y$ 轴上，函数 $y=\frac{2}{x}(x>0)$ 的图象与 $\mathit{DE}$ 交于点 $A$ ．若点 $B$ 是点 $A$ 的"倒数点"，且点 $B$ 在矩形 $\mathit{OCDE}$ 的一边上，则 $\mathit{\Delta OBC}$ 的面积为 　　．

如图，在平面直角坐标系中，矩形 $\mathit{ABCD}$的对角线 $\mathit{AC}$的中点与坐标原点重合，点 $E$是 $x$轴上一点，连接 $\mathit{AE}$．若 $\mathit{AD}$平分 $\angle \mathit{OAE}$，反比例函数 $y=\frac{k}{x}(k>0,x>0)$的图象经过 $\mathit{AE}$上的两点 $A$， $F$，且 $\mathit{AF}=\mathit{EF}$， $\mathit{\Delta ABE}$的面积为18，则 $k$的值为 $($　　 $)$

A．6B．12C．18D．24

如图， $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ACB}=90°$，顶点 $A$， $B$都在反比例函数 $y=\frac{k}{x}(x>0)$的图象上，直线 $\mathit{AC}\perp x$轴，垂足为 $D$，连结 $\mathit{OA}$， $\mathit{OC}$，并延长 $\mathit{OC}$交 $\mathit{AB}$于点 $E$，当 $\mathit{AB}=2\mathit{OA}$时，点 $E$恰为 $\mathit{AB}$的中点，若 $\angle \mathit{AOD}=45°$， $\mathit{OA}=2\sqrt{2}$．

（1）求反比例函数的解析式；

（2）求 $\angle \mathit{EOD}$的度数．

设 $A$， $B$， $C$， $D$是反比例函数 $y=\frac{k}{x}$图象上的任意四点，现有以下结论：

①四边形 $\mathit{ABCD}$可以是平行四边形；

②四边形 $\mathit{ABCD}$可以是菱形；

③四边形 $\mathit{ABCD}$不可能是矩形；

④四边形 $\mathit{ABCD}$不可能是正方形．

其中正确的是　　．（写出所有正确结论的序号）

若点 $A(-1,y_1)$， $B(2,y_2)$， $C(3,y_3)$在反比例函数 $y=-\frac{6}{x}$的图象上，则 $y_1$， $y_2$， $y_3$的大小关系是 $($　　 $)$

A． $y_1>y_2>y_3$B． $y_2>y_3>y_1$C． $y_1>y_3>y_2$D． $y_3>y_2>y_1$

从 $-1$，2， $-3$，4这四个数中任取两个不同的数分别作为 $a$， $b$的值，得到反比例函数 $y=\frac{\mathit{ab}}{x}$，则这些反比例函数中，其图象在二、四象限的概率是　　．

在反比例函数 $y=\frac{k^2+1}{x}(k$ 为常数）上有三点 $A(x_1$ ， $y_1)$ ， $B(x_2$ ， $y_2)$ ， $C(x_3$ ， $y_3)$ ，若 $x_1<0<x_2<x_3$ ，则 $y_1$ ， $y_2$ ， $y_3$ 的大小关系为 $($ 　　 $)$

A．

$y_1<y_2<y_3$

B．

$y_2<y_1<y_3$

C．

$y_1<y_3<y_2$

D．

$y_3<y_2<y_1$

反比例函数 $y=\frac{k}{x}(k\ne 0)$的图象经过点 $A(-2,4)$，则在每一个象限内， $y$随 $x$的增大而　　．（填“增大”或“减小” $)$

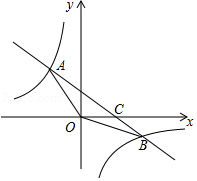
如图，在直角坐标系中，直线 $y_1=\mathit{ax}+b$与双曲线 $y_2=\frac{k}{x}(k\ne 0)$分别相交于第二、四象限内的 $A(m,4)$， $B(6,n)$两点，与 $x$轴相交于 $C$点．已知 $\mathit{OC}=3$， $\tan \angle \mathit{ACO}=\frac{2}{3}$．

（1）求 $y_1$， $y_2$对应的函数表达式；

（2）求 $\mathit{\Delta AOB}$的面积；

（3）直接写出当 $x<0$时，不等式 $\mathit{ax}+b>\frac{k}{x}$的解集．

已知点 $(-2$， $a\left)\right(2$， $b\left)\right(3$， $c)$在函数 $y=\frac{k}{x}(k>0)$的图象上，则下列判断正确的是 $($　　 $)$

A． $a<b<c$B． $b<a<c$C． $a<c<b$D． $c<b<a$

一次函数 $y=\mathit{ax}-a$与反比例函数 $y=\frac{a}{x}(a\ne 0)$在同一坐标系中的图象可能是 $($　　 $)$

A．B．

C．D．

关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．

甲：函数图象经过点 $(-1,1)$ ；

乙：函数图象经过第四象限；

丙：当 $x>0$ 时， $y$ 随 $x$ 的增大而增大．

则这个函数表达式可能是 $($ 　　 $)$

A．

$y=-x$

B．

$y=\frac{1}{x}$

C．

$y=x^2$

D．

$y=-\frac{1}{x}$

已知三个点 $(x_1$ ， $y_1)$ ， $(x_2$ ， $y_2)$ ， $(x_3$ ， $y_3)$ 在反比例函数 $y=\frac{2}{x}$ 的图象上，其中 $x_1<x_2<0<x_3$ ，下列结论中正确的是 $($ 　　 $)$

A．

$y_2<y_1<0<y_3$

B．

$y_1<y_2<0<y_3$

C．

$y_3<0<y_2<y_1$

D．

$y_3<0<y_1<y_2$