如图,△ ,△ ,△ , ,△ 都是斜边在 轴上的等腰直角三角形,点 , , , , 都在 轴上,点 , , , , 都在反比例函数 的图象上,则点 的坐标为 .(用含有正整数 的式子表示)

如图,在平面直角坐标系 中,已知直线 分别交反比例函数 和 在第一象限的图象于点 , ,过点 作 轴于点 ,交 的图象于点 ,连接 .若 是等腰三角形,则 的值是 .

在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 , 称为点 的"倒数点".如图,矩形 的顶点 为 ,顶点 在 轴上,函数 的图象与 交于点 .若点 是点 的"倒数点",且点 在矩形 的一边上,则 的面积为 .

如图,正方形 的顶点 , 在函数 的图象上,点 , 分别在 轴, 轴的正半轴上,当 的值改变时,正方形 的大小也随之改变.
(1)当 时,正方形 的边长等于 .
(2)当变化的正方形 与(1)中的正方形 有重叠部分时, 的取值范围是 .
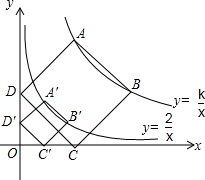
如图,点 为函数 图象上一点,连接 ,交函数 的图象于点 ,点 是 轴上一点,且 ,则 的面积为 .

已知点 、 都在反比例函数 的图象上,其横坐标分别是 、 .过点 分别向 轴、 轴作垂线,垂足分别是 、 ;过点 分别向 轴、 轴作垂线,垂足分别是 、 , 与 交于点 .当点 在线段 上、且 时, 的值等于 .
如图,已知直线 ,双曲线 ,在 上取一点 , ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,过 作 轴的垂线交双曲线于点 ,过 作 轴的垂线交 于点 ,此时 与 重合,并得到一个正方形 ,若原点 在正方形 的对角线上且分这条对角线为 的两条线段,则 的值为 .
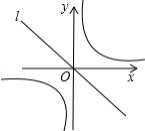
设 , , , 是反比例函数 图象上的任意四点,现有以下结论:
①四边形 可以是平行四边形;
②四边形 可以是菱形;
③四边形 不可能是矩形;
④四边形 不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
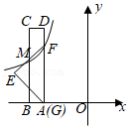
如图,将一把矩形直尺 和一块等腰直角三角板 摆放在平面直角坐标系中, 在 轴上,点 与点 重合,点 在 上, 交 于点 ,反比例函数 的图象恰好经过点 , ,若直尺的宽 ,三角板的斜边 ,则 .
反比例函数 的图象经过点 ,则在每一个象限内, 随 的增大而 .(填“增大”或“减小”
从 ,2, ,4这四个数中任取两个不同的数分别作为 , 的值,得到反比例函数 ,则这些反比例函数中,其图象在二、四象限的概率是 .