设 , , , 是反比例函数 图象上的任意四点,现有以下结论:
①四边形 可以是平行四边形;
②四边形 可以是菱形;
③四边形 不可能是矩形;
④四边形 不可能是正方形.
其中正确的是 .(写出所有正确结论的序号)
如图,点,
分别是正比例函数
的图象与反比例函数
的图象的交点,过
点作
轴于点
,过
点作
轴于点
,则四边形
的面积为 .

如图,在平面直角坐标系中,点,
在反比例函数
的图象上运动,且始终保持线段
的长度不变.
为线段
的中点,连接
.则线段
长度的最小值是 (用含
的代数式表示).

如图,在平面直角坐标系中,正方形的面积为4,边
、
分别在
轴、
轴上,一个反比例函数的图象经过点
.若该函数图象上的点
到
轴的距离是这个正方形边长的一半,则点
的坐标为 .

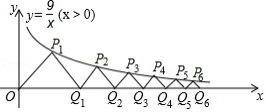
如图,在平面直角坐标系中,点
,
、
,
、
,
,
,
,
均在反比例函数
的图象上,点
、
、
、
、
均在
轴的正半轴上,且△
、△
、△
、
、△
均为等腰直角三角形,
、
、
、
、
分别为以上等腰直角三角形的底边,则
的值等于 .
如图,反比例函数经过
、
两点,过点
作
轴于点
,过点
作
轴于点
,过点
作
轴于点
,连结
,已知
、
、
.则
.

在-1,1,2这三个数中任选2个数分别作为P点的横坐标和纵坐标,过P点画双曲线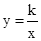 ,该双曲线位于第二、四象限的概率是 。
,该双曲线位于第二、四象限的概率是 。
(年新疆、生产建设兵团)若点P1(﹣1,m),P2(﹣2,n)在反比例函数 (
( )的图象上,则m n.(填“>”,“<”或“=”)
)的图象上,则m n.(填“>”,“<”或“=”)
如图,将一把矩形直尺 和一块等腰直角三角板 摆放在平面直角坐标系中, 在 轴上,点 与点 重合,点 在 上, 交 于点 ,反比例函数 的图象恰好经过点 , ,若直尺的宽 ,三角板的斜边 ,则 .
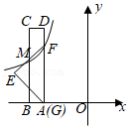
如图,已知在平面直角坐标系 中, 的直角顶点 在 轴的正半轴上,点 在第一象限,反比例函数 的图象经过 的中点 .交 于点 ,连结 .若 的面积是2,则 的值是 .

已知反比例函数 的图象在第一、三象限内,则 的值可以是 .(写出满足条件的一个 的值即可)