如图,在平面直角坐标系中,抛物线与
轴相交于
,
两点,与
轴相交于点
,顶点为
,直线
与
轴相交于点
.
(1)当时,抛物线顶点
的坐标为 ,
;
(2)的长是否与
值有关,说明你的理由;
(3)设,
,求
的取值范围;
(4)以为斜边,在直线
的左下方作等腰直角三角形
.设
,直接写出
关于
的函数解析式及自变量
的取值范围.

某厂按用户的月需求量(件
完成一种产品的生产,其中
,每件的售价为18万元,每件的成本
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(件
成反比,经市场调研发现,月需求量
与月份
为整数,
,符合关系式
为常数),且得到了表中的数据.
月份 |
1 |
2 |
成本 |
11 |
12 |
需求量 |
120 |
100 |
(1)求与
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第个月和第
个月的利润相差最大,求
.
在平面直角坐标系中的点
和图形
,给出如下的定义:若在图形
上存在一点
,使得
、
两点间的距离小于或等于1,则称
为图形
的关联点.
(1)当的半径为2时,
①在点,
,
,
,
,
中,
的关联点是 .
②点在直线
上,若
为
的关联点,求点
的横坐标的取值范围.
(2)的圆心在
轴上,半径为2,直线
与
轴、
轴交于点
、
.若线段
上的所有点都是
的关联点,直接写出圆心
的横坐标的取值范围.
某农作物的生长率与温度
有如下关系:如图1,当
时可近似用函数
刻画;当
时可近似用函数
刻画.
(1)求的值.
(2)按照经验,该作物提前上市的天数(天
与生长率
满足函数关系:
生长率 |
0.2 |
0.25 |
0.3 |
0.35 |
提前上市的天数 |
0 |
5 |
10 |
15 |
①请运用已学的知识,求关于
的函数表达式;
②请用含的代数式表示
.
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本
(元
与大棚温度
之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).
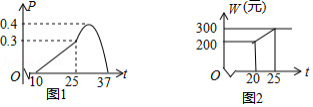
学校数学兴趣小组利用机器人开展数学活动.
在相距150个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.
兴趣小组成员探究这两个机器人迎面相遇的情况,这里的”迎面相遇“包括面对面相遇、在端点处相遇这两种.
(观察)
①观察图1,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为30个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为40个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图2所示).
① ;
②分别求出各部分图象对应的函数表达式,并在图2中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.
若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过60个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是 .(直接写出结果)

红星公司销售一种成本为40元 件产品,若月销售单价不高于50元 件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为 (单位:元 件),月销售量为 (单位:万件).
(1)直接写出 与 之间的函数关系式,并写出自变量 的取值范围;
(2)当月销售单价是多少元时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款 元.已知该公司捐款当月的月销售单价不高于70元 件,月销售最大利润是78万元,求 的值.
为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买 种花卉与用900元购买 种花卉的数量相等,且 种花卉每盆比 种花卉多0.5元.
(1) , 两种花卉每盆各多少元?
(2)计划购买 , 两种花卉共6000盆,其中 种花卉的数量不超过 种花卉数量的 ,求购买 种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?
某品牌鞋子的长度 与鞋子的"码"数 之间满足一次函数关系.若22码鞋子的长度为 ,44码鞋子的长度为 ,则38码鞋子的长度为
| A. |
|
B. |
|
C. |
|
D. |
|
为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液,经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.
(1)求甲、乙两种消毒液的零售价分别是每桶多少元?
(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的 .由于购买量大,甲、乙两种消毒液分别获得了20元 桶、15元 桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
下面图片是七年级教科书中“实际问题与一元一次方程”的探究3.
 探究3
探究3
电话计费问题
下表中有两种移动电话计费方式.
月使用费 元 |
主叫限定时间 |
主叫超时费 (元 |
被叫 |
|
方式一 |
58 |
150 |
0.25 |
免费 |
方式二 |
88 |
350 |
0.19 |
免费 |
考虑下列问题:
月使用费固定收: 主叫不超限定时间不再收费,主叫超时部分加收超时费,被叫免费. |
(1)设一个月内用移动电话主叫为 是正整数).根据上表,列表说明:当 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
小明升入初三再看这个问题,发现两种计费方式,每一种都是因主叫时间的变化而引起计费的变化,他把主叫时间视为在正实数范围内变化,决定用函数来解决这个问题.
(1)根据函数的概念,小明首先将问题中的两个变量分别设为自变量 和自变量的函数 ,请你帮小明写出:
表示问题中的 , 表示问题中的 .
并写出计费方式一和二分别对应的函数解析式;
(2)在给出的正方形网格纸上画出(1)中两个函数的大致图象,并依据图象写出如何根据主叫时间选择省钱的计费方式.(注 坐标轴单位长度可根据需要自己确定)


某通讯公司就手机流量套餐推出三种方案,如下表:
| |
方案 |
方案 |
方案 |
| 每月基本费用(元 |
20 |
56 |
266 |
| 每月免费使用流量(兆 |
1024 |
|
无限 |
| 超出后每兆收费(元 |
|
|
|
, , 三种方案每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系如图所示.
(1)请写出 , 的值.
(2)在 方案中,当每月使用的流量不少于1024兆时,求每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择 方案最划算?

某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现,每天销售量 (瓶 与每瓶售价 (元 之间存在一次函数关系(其中 ,且 为整数).当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶.
(1)求 与 之间的函数关系式;
(2)设该药店销售该消毒液每天的销售利润为 元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大,最大利润是多少元?
甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离 (米 与乙出发的时间 (秒 之间的函数关系如图所示,则下列结论正确的个数是
①乙的速度为5米 秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是 ;
④乙到达终点时,甲距离终点还有68米.

| A. |
4 |
B. |
3 |
C. |
2 |
D. |
1 |
李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 (千米)与行驶时间 (小时)的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升 千米,请根据图象解答下列问题:
(1)写出工厂离目的地的路程;
(2)求 关于 的函数表达式;
(3)当货车显示加油提醒后,问行驶时间 在怎样的范围内货车应进站加油?
