为庆祝"中国共产党的百年华诞",某校请广告公司为其制作"童心向党"文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的5倍,广告公司制作每件产品所需时间和利润如表:
| 产品 |
展板 |
宣传册 |
横幅 |
| 制作一件产品所需时间(小时) |
1 |
|
|
| 制作一件产品所获利润(元 |
20 |
3 |
10 |
(1)若制作三种产品共计需要25小时,所获利润为450元,求制作展板、宣传册和横幅的数量;
(2)若广告公司所获利润为700元,且三种产品均有制作,求制作三种产品总量的最小值.
如图,公交车行驶在笔直的公路上,这条路上有 , , , 四个站点,每相邻两站之间的距离为5千米,从 站开往 站的车称为上行车,从 站开往 站的车称为下行车,第一班上行车、下行车分别从 站、 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 , 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米 小时.

(1)问第一班上行车到 站、第一班下行车到 站分别用时多少?
(2)若第一班上行车行驶时间为 小时,第一班上行车与第一班下行车之间的距离为 千米,求 与 的函数关系式;
(3)一乘客前往 站办事,他在 , 两站间的 处(不含 , 站),刚好遇到上行车, 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到 站乘下行车前往 站.若乘客的步行速度是5千米 小时,求 满足的条件.
如图,在 中, , , ,点 为边 的中点.动点 从点 出发,沿折线 以每秒1个单位长度的速度向点 运动,当点 不与点 、 重合时,连结 .作点 关于直线 的对称点 ,连结 、 .设点 的运动时间为 秒.
(1)线段 的长为 ;
(2)用含 的代数式表示线段 的长;
(3)当点 在 内部时,求 的取值范围;
(4)当 与 相等时,直接写出 的值.

如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点 始终以 的速度在离地面 高的上空匀速向右飞行,2号试飞机(看成点 一直保持在1号机 的正下方.2号机从原点 处沿 仰角爬升,到 高的 处便立刻转为水平飞行,再过 到达 处开始沿直线 降落,要求 后到达 处.
(1)求 的 关于 的函数解析式,并直接写出2号机的爬升速度;
(2)求 的 关于 的函数解析式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离 不超过 的时长是多少.
注:(1)及(2)中不必写 的取值范围

如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在点 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.

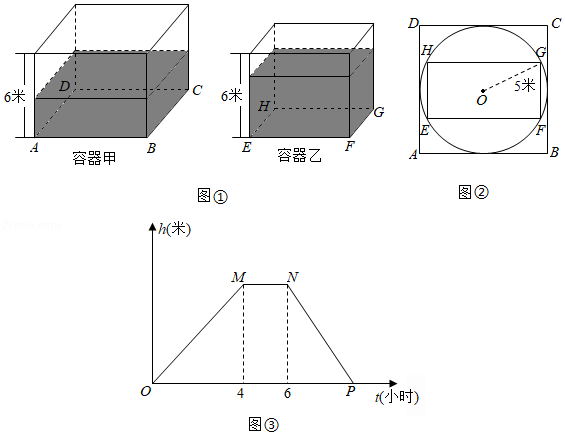
如图①,甲、乙都是高为6米的长方体容器,容器甲的底面 是正方形,容器乙的底面 是矩形.如图②,已知正方形 与矩形 满足如下条件:正方形 外切于一个半径为5米的圆 ,矩形 内接于这个圆 , .
(1)求容器甲、乙的容积分别为多少立方米?
(2)现在我们分别向容器甲、乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米 小时,4小时后,把容器甲的注水流量增加 立方米 小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米 小时,同时容器乙的注水流量仍旧保持不变,直到两个容器的水位高度相同,停止注水.在整个注水过程中,当注水时间为 时,我们把容器甲的水位高度记为 ,容器乙的水位高度记为 ,设 ,已知 (米 关于注水时间 (小时)的函数图象如图③所示,其中 平行于横轴,根据图中所给信息,解决下列问题:
①求 的值;
②求图③中线段 所在直线的解析式.
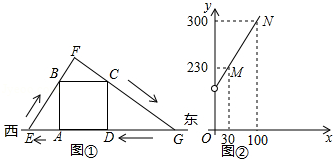
如图①,直线 表示一条东西走向的笔直公路,四边形 是一块边长为100米的正方形草地,点 , 在直线 上,小明从点 出发,沿公路 向西走了若干米后到达点 处,然后转身沿射线 方向走到点 处,接着又改变方向沿射线 方向走到公路 上的点 处,最后沿公路 回到点 处.设 米(其中 , 米,已知 与 之间的函数关系如图②所示,
(1)求图②中线段 所在直线的函数表达式;
(2)试问小明从起点 出发直至最后回到点 处,所走过的路径(即 是否可以是一个等腰三角形?如果可以,求出相应 的值;如果不可以,说明理由.
超市购进某种苹果,如果进价增加2元 千克要用300元;如果进价减少2元 千克,同样数量的苹果只用200元.
(1)求苹果的进价;
(2)如果购进这种苹果不超过100千克,就按原价购进;如果购进苹果超过100千克,超过部分购进价格减少2元 千克,写出购进苹果的支出 (元 与购进数量 (千克)之间的函数关系式;
(3)超市一天购进苹果数量不超过300千克,且购进苹果当天全部销售完,据统计,销售单价 (元 千克)与一天销售数量 (千克)的关系为 .在(2)的条件下,要使超市销售苹果利润 (元 最大,求一天购进苹果数量.(利润 销售收入 购进支出)
学校数学兴趣小组利用机器人开展数学活动.
在相距150个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.
兴趣小组成员探究这两个机器人迎面相遇的情况,这里的”迎面相遇“包括面对面相遇、在端点处相遇这两种.
(观察)
①观察图1,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为30个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为40个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(发现)
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图2所示).
① ;
②分别求出各部分图象对应的函数表达式,并在图2中补全函数图象;
(拓展)
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.
若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过60个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是 .(直接写出结果)

某商贸公司购进某种商品的成本为20元 ,经过市场调研发现,这种商品在未来40天的销售单价 (元 与时间 (天 之间的函数关系式为: ,且日销量 与时间 (天 之间的变化规律符合一次函数关系,如下表:
时间 (天 |
1 |
3 |
6 |
10 |
|
日销量 |
142 |
138 |
132 |
124 |
|
(1)填空: 与 的函数关系为 ;
(2)哪一天的销售利润最大?最大日销售利润是多少?
(3)在实际销售的前20天中,公司决定每销售 商品就捐赠 元利润 给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间 的增大而增大,求 的取值范围.
某公司生产的一种营养品信息如表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
| 营养品信息表 |
||
| 营养成份 |
每千克含铁42毫克 |
|
| 配料表 |
原料 |
每千克含铁 |
| 甲食材 |
50毫克 |
|
| 乙食材 |
10毫克 |
|
| 规格 |
每包食材含量 |
每包单价 |
| 包装 |
1千克 |
45元 |
| 包装 |
0.25千克 |
12元 |
(1)问甲、乙两种食材每千克进价分别是多少元?
(2)该公司每日用18000元购进甲、乙两种食材并恰好全部用完.
①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若 的数量不低于 的数量,则 为多少包时,每日所获总利润最大?最大总利润为多少元?
如图,以菱形 对角线交点为坐标原点,建立平面直角坐标系, 、 两点的坐标分别为 , 、 ,直线 交 于 ,动点 从点 出发,以每秒2个单位的速度沿着 的路线向终点 匀速运动,设 的面积为 ,点 的运动时间为 秒.
(1)求直线 的解析式;
(2)求 与 之间的函数关系式,并写出自变量 的取值范围;
(3)当 为何值时, ?并求出此时直线 与直线 所夹锐角的正切值.

公路上正在行驶的甲车,发现前方 处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程 (单位: 、速度 (单位: 与时间 (单位: 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至 时,它行驶的路程是多少?
(2)若乙车以 的速度匀速行驶,两车何时相距最近,最近距离是多少?
红星公司销售一种成本为40元 件产品,若月销售单价不高于50元 件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为 (单位:元 件),月销售量为 (单位:万件).
(1)直接写出 与 之间的函数关系式,并写出自变量 的取值范围;
(2)当月销售单价是多少元时,月销售利润最大,最大利润是多少万元?
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款 元.已知该公司捐款当月的月销售单价不高于70元 件,月销售最大利润是78万元,求 的值.
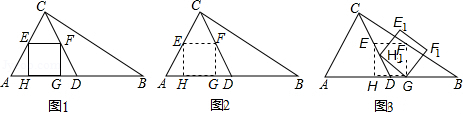
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.