我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 万元.(利润 销售额 种植成本)
、 两地相距 ,甲乙两人沿同一条路线从 地到 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以 的速度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开 地的距离 与时间 的关系如图所示,则甲出发 小时后和乙相遇.

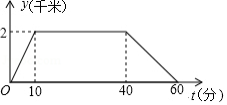
某日上午,甲,乙两车先后从 地出发沿同一条公路匀速前往 地,甲车8点出发,如图是其行驶路程 (千米)随行驶时间 (小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度 (单位:千米 小时)的范围是 .

在一条笔直的公路上有 、 、 三地, 地位于 、 两地之间,甲车从 地沿这条公路匀速驶向 地,乙车从 地沿这条公路匀速驶向 地.在甲车出发至甲车到达 地的过程中,甲、乙两车各自与 地的距离 与甲车行驶时间 之间的函数关系如图所示.下列结论:①甲车出发 时,两车相遇;②乙车出发 时,两车相距 ;③乙车出发 时,两车相遇;④甲车到达 地时,两车相距 .其中正确的是 (填写所有正确结论的序号).

一辆汽车由 地开往 地,它距离 地的路程 与行驶时间 的关系如图所示,如果汽车一直快速行驶,那么可以提前 小时到达 地.

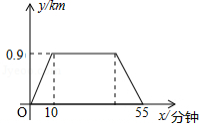
星期天,小明上午 从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离 (千米)与时间 (分钟)的关系如图所示,则上午 小明离家的距离是 千米.
甲、乙两动点分别从线段 的两端点同时出发,甲从点 出发,向终点 运动,乙从点 出发,向终点 运动.已知线段 长为 ,甲的速度为 .设运动时间为 ,甲、乙两点之间的距离为 , 与 的函数图象如图所示,则图中线段 所表示的函数关系式为 .(并写出自变量取值范围)

, 两地相距 ,甲货车从 地以 的速度匀速前往 地,到达 地后停止.在甲出发的同时,乙货车从 地沿同一公路匀速前往 地,到达 地后停止.两车之间的路程 与甲货车出发时间 之间的函数关系如图中的折线 所示.其中点 的坐标是 ,点 的坐标是 ,则点 的坐标是 .

在一条笔直的公路上有 , , 三地, 地位于 , 两地之间,甲,乙两车分别从 , 两地出发,沿这条公路匀速行驶至 地停止.从甲车出发至甲车到达 地的过程,甲、乙两车各自与 地的距离 与甲车行驶时间 之间的函数关系如图表示,当甲车出发 时,两车相距 .

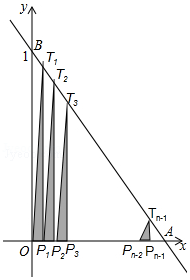
如图,直线 与两坐标轴分别交于 , 两点,将线段 分成 等份,分点分别为 , , , , ,过每个分点作 轴的垂线分别交直线 于点 , , , , ,用 , , , , 分别表示 △ , △ , , △ 的面积,则 .
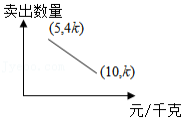
某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本5元 千克,现以8元卖出,挣得 元.
如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为 .

小明从家步行到学校需走的路程为1800米.图中的折线 反映了小明从家步行到学校所走的路程 (米 与时间 (分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.

小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .