初中数学一次函数的应用试题

4月23日是“世界读书日”，甲、乙两个书店在这一天举行了购书优惠活动．

甲书店：所有书籍按标价8折出售；

乙书店：一次购书中标价总额不超过100元的按原价计费，超过100元后的部分打6折．

（1）以 $x$（单位：元）表示标价总额， $y$（单位：元）表示应支付金额，分别就两家书店的优惠方式，求 $y$关于 $x$的函数解析式；

（2）“世界读书日”这一天，如何选择这两家书店去购书更省钱？

某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售．已知西瓜的成本为6元千克，规定销售单价不低于成本，又不高于成本的两倍．经过市场调查发现，某天西瓜的销售量（千克）与销售单价（元千克）的函数关系如图所示：

（1）求与的函数解析式（也称关系式）；

（2）求这一天销售西瓜获得的利润的最大值．

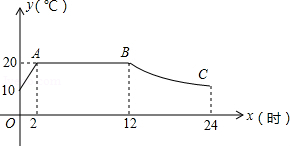
我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为 $15-{20}^{°}\text{C}$的新品种，如图是某天恒温系统从开启到关闭及关闭后，大棚里温度 $y{(}^{°}\text{C})$随时间 $x\left(h\right)$变化的函数图象，其中 $\mathit{AB}$段是恒温阶段， $\mathit{BC}$段是双曲线 $y=\frac{k}{x}$的一部分，请根据图中信息解答下列问题：

（1）求 $k$的值；

（2）恒温系统在一天内保持大棚里温度在 ${15}^{°}\text{C}$及 ${15}^{°}\text{C}$以上的时间有多少小时？

某公司计划购买，两种型号的电脑，已知购买一台型电脑需0.6万元，购买一台型电脑需0.4万元，该公司准备投入资金万元，全部用于购进35台这两种型号的电脑，设购进型电脑台．

（1）求关于的函数解析式；

（2）若购进型电脑的数量不超过型电脑数量的2倍，则该公司至少需要投入资金多少万元？

蚊香长度 $y$（厘米）与燃烧时间 $t$（小时）之间的函数表达式为 $y=105-10t$．则蚊香燃烧的速度是 $($　　 $)$

A．10厘米 $/$小时B．105厘米 $/$小时

C．10.5厘米 $/$小时D．不能确定

甲、乙两个批发店销售同一种苹果，在甲批发店，不论一次购买数量是多少，价格均为6元．在乙批发店，一次购买数量不超过时，价格为7元；一次购买数量超过时，其中有的价格仍为7元，超过部分的价格为5元．设小王在同一个批发店一次购买苹果的数量为．

（Ⅰ）根据题意填表：

一次购买数量	30	50	150
甲批发店花费元		300
乙批发店花费元		350

（Ⅱ）设在甲批发店花费元，在乙批发店花费元，分别求，关于的函数解析式；

（Ⅲ）根据题意填空：

①若小王在甲批发店和在乙批发店一次购买苹果的数量相同，且花费相同，则他在同一个批发店一次购买苹果的数量为　　；

②若小王在同一个批发店一次购买苹果的数量为，则他在甲、乙两个批发店中的　　批发店购买花费少；

③若小王在同一个批发店一次购买苹果花费了360元，则他在甲、乙两个批发店中的　　批发店购买数量多．

如图中的折线 $\mathit{ABC}$表示某汽车的耗油量 $y$（单位： $L/\mathit{km})$与速度 $x$（单位： $\mathit{km}/h)$之间的函数关系 $(30⩽x⩽120)$，已知线段 $\mathit{BC}$表示的函数关系中，该汽车的速度每增加 $1\mathit{km}/h$，耗油量增加 $0.002L/\mathit{km}$．

（1）当速度为 $50\mathit{km}/h$、 $100\mathit{km}/h$时，该汽车的耗油量分别为　 $L/\mathit{km}$、　　 $L/\mathit{km}$．

（2）求线段 $\mathit{AB}$所表示的 $y$与 $x$之间的函数表达式．

（3）速度是多少时，该汽车的耗油量最低？最低是多少？

甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

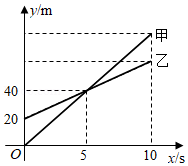
A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元     $)$	20	56	266
每月免费使用流量（兆     $)$	1024	$m$	无限
超出后每兆收费（元     $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

某品牌鞋子的长度 $\mathit{ycm}$ 与鞋子的"码"数 $x$ 之间满足一次函数关系．若22码鞋子的长度为 $16\mathit{cm}$ ，44码鞋子的长度为 $27\mathit{cm}$ ，则38码鞋子的长度为 $($ 　　 $)$

A．

$23\mathit{cm}$

B．

$24\mathit{cm}$

C．

$25\mathit{cm}$

D．

$26\mathit{cm}$

下面图片是七年级教科书中“实际问题与一元一次方程”的探究3．

探究3

电话计费问题

下表中有两种移动电话计费方式．

	月使用费 $/$元	主叫限定时间 $/\mathit{min}$	主叫超时费 $/$（元 $/\mathit{min})$	被叫
方式一	58	150	0.25	免费
方式二	88	350	0.19	免费

考虑下列问题：

月使用费固定收： 主叫不超限定时间不再收费，主叫超时部分加收超时费，被叫免费．

（1）设一个月内用移动电话主叫为 $\mathit{tmin}(t$是正整数）．根据上表，列表说明：当 $t$在不同时间范围内取值时，按方式一和方式二如何计费．

（2）观察你的列表，你能从中发现如何根据主叫时间选择省钱的计费方式吗？通过计算验证你的看法．

小明升入初三再看这个问题，发现两种计费方式，每一种都是因主叫时间的变化而引起计费的变化，他把主叫时间视为在正实数范围内变化，决定用函数来解决这个问题．

（1）根据函数的概念，小明首先将问题中的两个变量分别设为自变量 $x$和自变量的函数 $y$，请你帮小明写出：

$x$表示问题中的 　　， $y$表示问题中的 　　．

并写出计费方式一和二分别对应的函数解析式；

（2）在给出的正方形网格纸上画出（1）中两个函数的大致图象，并依据图象写出如何根据主叫时间选择省钱的计费方式．（注 $:$坐标轴单位长度可根据需要自己确定）

暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下．

方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；

方案二：不购买学生暑期专享卡，每次健身费用按八折优惠．

设某学生暑期健身 $x$（次 $)$，按照方案一所需费用为 $y_1$（元 $)$，且 $y_1=k_{1}x+b$；按照方案二所需费用为 $y_2$（元 $)$，且 $y_2=k_{2}x$．其函数图象如图所示．

（1）求 $k_1$和 $b$的值，并说明它们的实际意义；

（2）求打折前的每次健身费用和 $k_2$的值；

（3）八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少？说明理由．

为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用 $y$（元 $)$与种植面积 $x\left(m^2\right)$之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．

（1）直接写出当 $0⩽x⩽300$和 $x>300$时， $y$与 $x$的函数关系式；

（2）广场上甲、乙两种花卉的种植面积共 $1200m^2$，若甲种花卉的种植面积不少于 $200m^2$，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？

甲、乙两人分别从 $A$， $B$两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到达 $B$地后，乙继续前行．设出发 $\mathit{xℎ}$后，两人相距 $\mathit{ykm}$，图中折线表示从两人出发至乙到达 $A$地的过程中 $y$与 $x$之间的函数关系．

根据图中信息，求：

（1）点 $Q$的坐标，并说明它的实际意义；

（2）甲、乙两人的速度．

荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）

（1）求桂味和糯米糍的售价分别是每千克多少元；

（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．