初中数学一次函数的应用试题

某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）满足如下关系：

月产销量 $y$（个）	$\dots$	160	200	240	300	$\dots$
每个玩具的固定成本 $Q$（元）	$\dots$	60	48	40	32	$\dots$

（1）写出月产销量 $y$（个）与销售单价 $x$（元）之间的函数关系式；

（2）求每个玩具的固定成本 $Q$（元）与月产销量 $y$（个）之间的函数关系式；

（3）若每个玩具的固定成本为30元，则它占销售单价的几分之几？

（4）若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

在一段长为1000的笔直道路AB上，甲、乙两名运动员均从A点出发进行往返跑训练．已知乙比甲先出发30秒钟，甲距A点的距离y（米）与其出发的时间x（分钟）的函数图象如图所示，乙的速度是150米/分钟，且当乙到达B点后立即按原速返回．

（1）当x为何值时，两人第一次相遇？

（2）当两人第二次相遇时，求甲的总路程．

小明从家步行到学校需走的路程为1800米．图中的折线 $\mathit{OAB}$反映了小明从家步行到学校所走的路程 $s$（米 $)$与时间 $t$（分钟）的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行　　米．

甲、乙施工队分别从两端修一段长度为380米的公路．在施工过程中，乙队曾因技术改进而停工一天，之后加快了施工进度并与甲队共同按期完成了修路任务．下表是根据每天工程进度绘制而成的．

施工时间 $/$ 天	1	2	3	4	5	6	7	8	9
累计完成施工量 $/$ 米	35	70	105	140	160	215	270	325	380

下列说法错误的是 $($ 　　 $)$

A．	甲队每天修路20米
B．	乙队第一天修路15米
C．	乙队技术改进后每天修路35米
D．	前七天甲，乙两队修路长度相等

星期天，李玉刚同学随爸爸妈妈回老家探望爷爷奶奶，爸爸 $\mathit{8}\mathit{:}\mathit{30}$骑自行车先走，平均每小时骑行 $\mathit{20}\mathit{km}$；李玉刚同学和妈妈 $\mathit{9}\mathit{:}\mathit{30}$乘公交车后行，公交车平均速度是 $\mathit{40}\mathit{km}\mathit{/}\mathit{h}$．爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同，路程均为 $\mathit{40}\mathit{km}$．设爸爸骑行时间为 $\mathit{x}\mathit{\left(}\mathit{h}\mathit{\right)}$．

（1）请分别写出爸爸的骑行路程 ${\mathit{y}}_{\mathit{1}}\mathit{\left(}\mathit{km}\mathit{\right)}$、李玉刚同学和妈妈的乘车路程 ${\mathit{y}}_{\mathit{2}}\mathit{\left(}\mathit{k}\mathit{m}\mathit{\right)}$与 $\mathit{x}\mathit{\left(}\mathit{h}\mathit{\right)}$之间的函数解析式，并注明自变量的取值范围；

（2）请在同一个平面直角坐标系中画出（1）中两个函数的图象；

（3）请回答谁先到达老家．

汛期到来，山洪暴发．下表记录了某水库内水位的变化情况，其中表示时间（单位：，表示水位高度（单位：，当时，达到警戒水位，开始开闸放水．

	0	2	4	6	8	10	12	14	16	18	20
	14	15	16	17	18	14.4	12	10.3	9	8	7.2

（1）在给出的平面直角坐标系中，根据表格中的数据描出相应的点．

（2）请分别求出开闸放水前和放水后最符合表中数据的函数解析式．

（3）据估计，开闸放水后，水位的这种变化规律还会持续一段时间，预测何时水位达到．

“和谐号”火车从车站出发，在行驶过程中速度 $y$（单位： $m/s)$与时间 $x$（单位： $s)$的关系如图所示，其中线段 $\mathit{BC}//x$轴．

请根据图象提供的信息解答下列问题：

（1）当 $0⩽x⩽10$，求 $y$关于 $x$的函数解析式；

（2）求 $C$点的坐标．

甲无人机从地面起飞，乙无人机从距离地面 $20m$ 高的楼顶起飞，两架无人机同时匀速上升 $10s$ ．甲、乙两架无人机所在的位置距离地面的高度 $y$ （单位： $m)$ 与无人机上升的时间 $x$ （单位： $s)$ 之间的关系如图所示．下列说法正确的是 $($ 　　 $)$

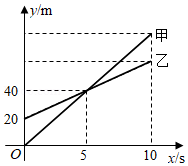
A．	$5s$ 时，两架无人机都上升了 $40m$
B．	$10s$ 时，两架无人机的高度差为 $20m$
C．	乙无人机上升的速度为 $8m/s$
D．	$10s$ 时，甲无人机距离地面的高度是 $60m$

某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元     $)$	20	56	266
每月免费使用流量（兆     $)$	1024	$m$	无限
超出后每兆收费（元     $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

某品牌鞋子的长度 $\mathit{ycm}$ 与鞋子的"码"数 $x$ 之间满足一次函数关系．若22码鞋子的长度为 $16\mathit{cm}$ ，44码鞋子的长度为 $27\mathit{cm}$ ，则38码鞋子的长度为 $($ 　　 $)$

A．

$23\mathit{cm}$

B．

$24\mathit{cm}$

C．

$25\mathit{cm}$

D．

$26\mathit{cm}$

下面图片是七年级教科书中“实际问题与一元一次方程”的探究3．

探究3

电话计费问题

下表中有两种移动电话计费方式．

	月使用费 $/$元	主叫限定时间 $/\mathit{min}$	主叫超时费 $/$（元 $/\mathit{min})$	被叫
方式一	58	150	0.25	免费
方式二	88	350	0.19	免费

考虑下列问题：

月使用费固定收： 主叫不超限定时间不再收费，主叫超时部分加收超时费，被叫免费．

（1）设一个月内用移动电话主叫为 $\mathit{tmin}(t$是正整数）．根据上表，列表说明：当 $t$在不同时间范围内取值时，按方式一和方式二如何计费．

（2）观察你的列表，你能从中发现如何根据主叫时间选择省钱的计费方式吗？通过计算验证你的看法．

小明升入初三再看这个问题，发现两种计费方式，每一种都是因主叫时间的变化而引起计费的变化，他把主叫时间视为在正实数范围内变化，决定用函数来解决这个问题．

（1）根据函数的概念，小明首先将问题中的两个变量分别设为自变量 $x$和自变量的函数 $y$，请你帮小明写出：

$x$表示问题中的 　　， $y$表示问题中的 　　．

并写出计费方式一和二分别对应的函数解析式；

（2）在给出的正方形网格纸上画出（1）中两个函数的大致图象，并依据图象写出如何根据主叫时间选择省钱的计费方式．（注 $:$坐标轴单位长度可根据需要自己确定）

暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下．

方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；

方案二：不购买学生暑期专享卡，每次健身费用按八折优惠．

设某学生暑期健身 $x$（次 $)$，按照方案一所需费用为 $y_1$（元 $)$，且 $y_1=k_{1}x+b$；按照方案二所需费用为 $y_2$（元 $)$，且 $y_2=k_{2}x$．其函数图象如图所示．

（1）求 $k_1$和 $b$的值，并说明它们的实际意义；

（2）求打折前的每次健身费用和 $k_2$的值；

（3）八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少？说明理由．

为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用 $y$（元 $)$与种植面积 $x\left(m^2\right)$之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．

（1）直接写出当 $0⩽x⩽300$和 $x>300$时， $y$与 $x$的函数关系式；

（2）广场上甲、乙两种花卉的种植面积共 $1200m^2$，若甲种花卉的种植面积不少于 $200m^2$，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？

甲、乙两人分别从 $A$， $B$两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到达 $B$地后，乙继续前行．设出发 $\mathit{xℎ}$后，两人相距 $\mathit{ykm}$，图中折线表示从两人出发至乙到达 $A$地的过程中 $y$与 $x$之间的函数关系．

根据图中信息，求：

（1）点 $Q$的坐标，并说明它的实际意义；

（2）甲、乙两人的速度．

荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）

（1）求桂味和糯米糍的售价分别是每千克多少元；

（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．