暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身 (次 ,按照方案一所需费用为 (元 ,且 ;按照方案二所需费用为 (元 ,且 .其函数图象如图所示.
(1)求 和 的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.

相关知识点
推荐套卷

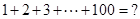
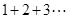
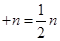
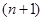 ,其中
,其中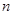 是正整数.
是正整数.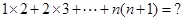

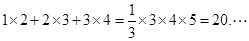
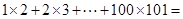 ___________________ ;
___________________ ; 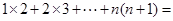 ______________________ ;
______________________ ;  ___________ .
___________ . 粤公网安备 44130202000953号
粤公网安备 44130202000953号