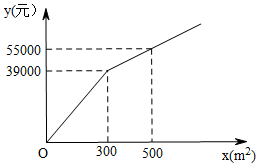
为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用 （元 与种植面积 之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元．
（1）直接写出当 和 时， 与 的函数关系式；
（2）广场上甲、乙两种花卉的种植面积共 ，若甲种花卉的种植面积不少于 ，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少？最少总费用为多少元？
相关试题
（本题8分）解方程
解：当
时，原方程化为
，
解得
，
（不合题意，舍去）
当
时，原方程化为
解得
（不合题意，舍去），
，
所以原方程的解为，，
请你依据以上提供的信息解法，解方程
， AB=2
，求∠BAC的度数．（本题6分）在如图所示的平面直角坐标系中，有△ABC．
（1）将△ABC向x轴负半轴方向平移4个单位得到△A1B1C1，画出图形并写出点A1的坐标．
（2）以原点O为旋转中心，将△ABC顺时针旋转90°后得到△A2B2C2，画出图形并写出点A2的坐标．
（3）△A2B2C2可以看作是由△A1B1C1先向右平移4个单位，然后以原点O为旋转中心，顺时针旋转90°得到的．除此之外，△A2B2C2还可以由△A1B1C1经过旋转变换得到，请在图中找出旋转中心．
，其中
，
.相关知识点
推荐套卷
粤公网安备 44130202000953号