小明学了勾股定理后很高兴,兴冲冲的回家告诉了爸爸:在△ABC 中,若∠C=90°, BC =" a" , AC =" b" , AB=c,如下图,根据勾股定理,则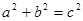 。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想
。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想 与
与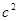 的关系,并选择其中一种情况给予证明。〔下图备用)
的关系,并选择其中一种情况给予证明。〔下图备用)
相关知识点
推荐套卷
小明学了勾股定理后很高兴,兴冲冲的回家告诉了爸爸:在△ABC 中,若∠C=90°, BC =" a" , AC =" b" , AB=c,如下图,根据勾股定理,则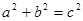 。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想
。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想 与
与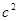 的关系,并选择其中一种情况给予证明。〔下图备用)
的关系,并选择其中一种情况给予证明。〔下图备用)