(本小题满分12分)如下图,给出了一个程序框图,其作用是输入 的值,输出相应的
的值,输出相应的 的值,
的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视 为自变量,
为自变量, 为函数值,试写出函数
为函数值,试写出函数 的解析式;
的解析式;
(Ⅲ)若要使输入的 的值与输出的
的值与输出的 的值相等,求输入
的值相等,求输入 的值的集合
的值的集合
(本小题满分12分)如图,设P是圆 上的动点,点D是P在x轴上的射影,M为PD上一点,且
上的动点,点D是P在x轴上的射影,M为PD上一点,且

(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为 的直线被轨迹C所截线段的长度。
的直线被轨迹C所截线段的长度。
(本小题满分12分)已知关于x的二次函数f(x)=ax2-4bx+1.
(1)设集合P={-1,1,2 ,3,4,5}和Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
,3,4,5}和Q={-2,-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率; 增函数的概率.
增函数的概率.
(本小题满分14分)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆 。
。
(1)若椭圆 ,判断
,判断 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出 与
与 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆 相似且短半轴长为
相似且短半轴长为 的椭圆
的椭圆 的方程;若在椭圆
的方程;若在椭圆 上存在两点
上存在两点 、
、 关于直线
关于直线 对称,求实数
对称,求实数 的取值范围?
的取值范围?
(3)如图:直线 与两个“相似椭圆”
与两个“相似椭圆” 和
和 分别交于点
分别交于点 和点
和点 ,证明:
,证明:
有两个红球和两个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )
| A.“恰好有一个黑球”与“恰好有两个黑球” | B.“至少有一个黑球”与“都是红球” |
| C.“至少有一个黑球”与“都是黑球” | D.“至少有一个黑球”与“至 少有一个红球” 少有一个红球” |
设( ,
, ),(
),( ,
, ),…,(
),…,( ,
, )是变量
)是变量 和
和 的
的 个样本点,直线
个样本点,直线 是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的( )
是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的( )
A. 和 和 的相关系数为直线 的相关系数为直线 的斜率 的斜率 |
B. 和 和 的相关系数在0到1之间 的相关系数在0到1之间 |
C.当 为偶数时,分布在 为偶数时,分布在 两侧的样本点的个数一定相同 两侧的样本点的个数一定相同 |
D.直线 过点 过点 |
离心率为黄金比 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设 是优美椭圆,F、A分别是它的左焦点和右顶点,B是它的短轴的一个顶点,则
是优美椭圆,F、A分别是它的左焦点和右顶点,B是它的短轴的一个顶点,则 =( )
=( )
A. |
B. |
C. |
D. |
下列四个函数中,在 上是增函数的是 ( )
上是增函数的是 ( )
A. . . |
B. |
C.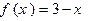 |
D.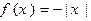 |
如图是正方体的平面展开图,在这个正方体中
⑴BM与 ED平行 ⑵CN与BE是异面
ED平行 ⑵CN与BE是异面 直线
直线
⑶CN与BM成60° ⑷DM与BN垂直
以上四个命题中,正确命题的序号是( )
| A.⑴⑵⑶ | B.⑵⑷ |
| C.⑶⑷ | D.⑵⑶⑷ |

有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三 棱锥形的铁架,则a的取值范围是 ( )
棱锥形的铁架,则a的取值范围是 ( )
| A.(0,+) | B.(1,2) |
| C.(-,+) | D.(0,2) |
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
⑴求正三棱柱的侧棱长.
⑵若M为BC1的中点,试用基向量 、
、 、
、 表示向量
表示向量 ;
;
⑶求异面直线AB1与BC所成角的余弦值.
如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.