给定下列函数:① ②
② ③
③ ④
④ ,其中在区间
,其中在区间
(0,1)上单调递减的函数的序号是( )
| A.① ② | B.② ③ | C.③ ④ | D.① ④ |
对实数 和
和 ,定义运算“
,定义运算“ ”:
”: 设函数
设函数 若函数
若函数 的图像与
的图像与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
下列说法错误的是 ( )
A.命题“若 ,则
,则 ”的逆否命题是:“若
”的逆否命题是:“若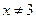 ,则
,则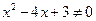 ”
”
B.“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
C.若 且
且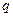 为假命题,则
为假命题,则 、
、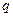 均为假命题
均为假命题
D.命题 :“∃
:“∃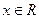 使得
使得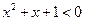 ”,则
”,则 ,均有
,均有 ”
”
设有一个回归方程为 ,则变量x增加一个单位时
,则变量x增加一个单位时
A. 平均增加1.5单位 B.
平均增加1.5单位 B.  平均增加2单
平均增加2单
C.  平均减少1.5单位
平均减少1.5单位 D.
D.  平均减少2单位
平均减少2单位
右图给出的是计算 的值的一个程序框图
的值的一个程序框图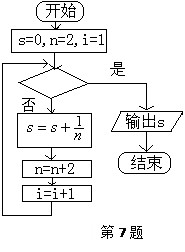
其中判断框内应填入的条件是( ) i>10
i>10  i<10
i<10  i>20
i>20  i
i <20
<20
若钝 角三角形三内角的度数成等差数列,且最大边长与最
角三角形三内角的度数成等差数列,且最大边长与最
小边长的比值为 ,则
,则 的范围是
的范围是
A.(1,2) B.(2,+∞) C.[3,+∞) D.(3,+∞)
(满分12分)) 设椭圆E: 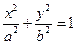 (a,b>0)过
(a,b>0)过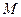 (2,
(2,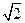 ) ,
) ,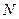 (
(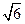 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.
(Ⅰ)求椭圆E的方程
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任 意一条切线与椭圆E恒有两个交点A,B,
意一条切线与椭圆E恒有两个交点A,B,
且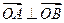 ?若存在,写
?若存在,写 出该圆的方程,并求|AB |的取值范围,若不存在说明理由
出该圆的方程,并求|AB |的取值范围,若不存在说明理由
设双曲线C: (a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
(a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为
A.   |
B.2 | C. |
D.3 |