[辽宁]2011年辽宁省辽南协作体高二上学期期中考试理科数学
下列说法错误的是 ( )
A.命题“若 ,则
,则 ”的逆否命题是:“若
”的逆否命题是:“若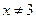 ,则
,则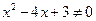 ”
”
B.“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
C.若 且
且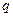 为假命题,则
为假命题,则 、
、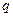 均为假命题
均为假命题
D.命题 :“∃
:“∃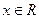 使得
使得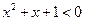 ”,则
”,则 ,均有
,均有 ”
”
“ ”是“对任意的正数
”是“对任意的正数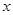 ,
,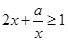 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
如果实数x,y满足x2+y2=1,则(1-xy) (1+xy)有
A.最小值 和最大值1 B.最小值
和最大值1 B.最小值 而无最大值
而无最大值
C.最大值1和最小值 D.最大值1而无最小值
D.最大值1而无最小值
设有一个回归方程为 ,则变量x增加一个单位时
,则变量x增加一个单位时
A. 平均增加1.5单位 B.
平均增加1.5单位 B.  平均增加2单
平均增加2单
C.  平均减少1.5单位
平均减少1.5单位 D.
D.  平均减少2单位
平均减少2单位
右图给出的是计算 的值的一个程序框图
的值的一个程序框图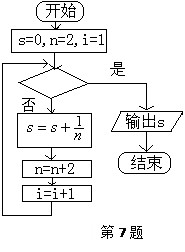
其中判断框内应填入的条件是( ) i>10
i>10  i<10
i<10  i>20
i>20  i
i <20
<20
若钝 角三角形三内角的度数成等差数列,且最大边长与最
角三角形三内角的度数成等差数列,且最大边长与最
小边长的比值为 ,则
,则 的范围是
的范围是
A.(1,2) B.(2,+∞) C.[3,+∞) D.(3,+∞)
 .为双曲线
.为双曲线 上的一点,
上的一点, 为一个焦点,以
为一个焦点,以 为直径的圆与圆
为直径的圆与圆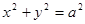 的位置关系是
的位置关系是 内切
内切  内切或外切
内切或外切  .外切
.外切  .相离或相交
.相离或相交
已知命题:“∃x∈[1,2],使x2+2x+a≥0”为真命题,则a的 取值范围是____________
取值范围是____________
在平面直角坐 标系中,双曲线的中心在原点,焦点在
标系中,双曲线的中心在原点,焦点在 轴上,一条渐近线方程为
轴上,一条渐近线方程为 ,则它的离心率为_____________
,则它的离心率为_____________
满分10分) 设有关于 的一元二次方程
的一元二次方程
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率
三个数中任取的一个数,求上述方程有实根的概率
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率
任取的一个数,求上述方程有实根的概率
(满分12分)已知命题 上
上 有且仅有一解;命题
有且仅有一解;命题 只有一个实数
只有一个实数 满足不等式
满足不等式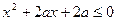 .若命题“
.若命题“ ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.
(满分12分)设锐角△ABC的内角A、B、C所对的边分别是a、b、c, ,
,
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围。
(满分12分)某家公司每 月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的
月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的 总量。
总量。
| 羊毛颜色 |
每 匹需要 / kg 匹需要 / kg |
供应量/ kg |
|
| 布料A |
布料B |
||
| 红 |
4 |
4 |
1400 |
| 绿 |
6 |
3 |
1800 |
| 黄 |
2 |
6 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最 大的利润是多少?
大的利润是多少?
 ,将这组数据中的每一个数据都乘以2,所得到的一组数据的
,将这组数据中的每一个数据都乘以2,所得到的一组数据的
 ;
; 
 ;
; 
 ;
; 
 和双曲线
和双曲线 有公共焦点,那么双曲线的渐近线方程为( )
有公共焦点,那么双曲线的渐近线方程为( )







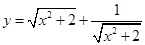 B.
B. 
 D.
D. 
 和
和 的前
的前 项和分别为
项和分别为 和
和 ,且
,且 ,则使得
,则使得 为整数的正整数
为整数的正整数 2
2 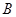 .3
.3  5
5  4
4 是椭圆
是椭圆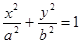
 的两个焦点,
的两个焦点, 是以
是以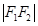 为直径的圆与椭圆的一个交点,且
为直径的圆与椭圆的一个交点,且 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( ) .
.
 .
.
 .
.
 .
.
 ≥0,b≥0,
≥0,b≥0, +
+ 的范围是_____________
的范围是_____________ 知抛物线
知抛物线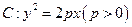 的准线为
的准线为 ,
, 过
过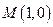 且斜率为
且斜率为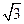 的直线
的直线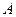 ,与
,与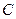 的一个交点为
的一个交点为 .若
.若 ,则
,则 _____________
_____________ 的各项均为正值,首项
的各项均为正值,首项 ,前n项和为
,前n项和为 ,且
,且
 的前n项和
的前n项和 .
.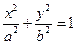 (a,b>0)过
(a,b>0)过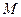 (2,
(2,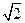 ) ,
) ,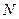 (
(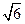 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点. 意一条切线与椭圆E恒有两个交点A,B,
意一条切线与椭圆E恒有两个交点A,B,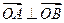 ?若存在,写
?若存在,写 粤公网安备 44130202000953号
粤公网安备 44130202000953号