(本小题满分14分)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆 。
。
(1)若椭圆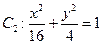 ,判断
,判断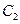 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出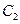 与
与 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆 相似且短半轴长为
相似且短半轴长为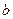 的椭圆
的椭圆 的方程;若在椭圆
的方程;若在椭圆 上存在两点
上存在两点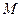 、
、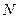 关于直线
关于直线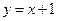 对称,求实数
对称,求实数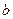 的取值范围?
的取值范围?
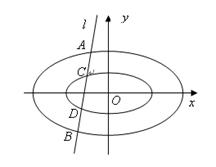
(3)如图:直线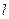 与两个“相似椭圆”
与两个“相似椭圆”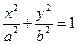 和
和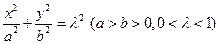 分别交于点
分别交于点 和点
和点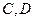 ,证明:
,证明: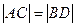
推荐套卷
 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.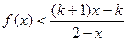
 满足
满足 ,且其图象在y轴上的截距为1,在x轴上截得的线段长为
,且其图象在y轴上的截距为1,在x轴上截得的线段长为 ,求
,求 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
 满足
满足 ,且
,且 。
。 上,
上, 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的范围。
的范围。 满足
满足 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号