已知双曲线 C:  , O为坐标原点, F为 C的右焦点,过 F的直线与 C的两条渐近线的交点分别为 M 、 N.若
OMN为直角三角形,则| MN|=( )
, O为坐标原点, F为 C的右焦点,过 F的直线与 C的两条渐近线的交点分别为 M 、 N.若
OMN为直角三角形,则| MN|=( )
| A. |
|
B. |
3 |
C. |
|
D. |
4 |
如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形 ABC的斜边 BC,直角边 AB, AC.△ ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III的概率分别记为 p 1, p 2, p 3,则( )

| A. |
p 1=p 2 |
B. |
p 1=p 3 |
| C. |
p 2=p 3 |
D. |
p 1=p 2+p 3 |
已知函数 .若 g( x)存在2个零点,则 a的取值范围是( )
| A. |
[-1,0) |
B. |
[0,+∞) |
C. |
[-1,+∞) |
D. |
[1,+∞) |
设抛物线 C: y 2=4 x的焦点为 F,过点(-2,0)且斜率为 的直线与 C交于 M, N两点,则 =( )
| A. |
5 |
B. |
6 |
C. |
7 |
D. |
8 |
某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点 在正视图上的对应点为 ,圆柱表面上的点 在左视图上的对应点为 ,则在此圆柱侧面上,从 到 的路径中,最短路径的长度为( )

| A. |
|
B. |
|
C. |
|
D. |
2 |
在△ 中, 为 边上的中线, 为 的中点,则 ( )
| A. |
|
B. |
|
| C. |
|
D. |
|
设函数
.若
为奇函数,则曲线 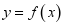 在点
处的切线方程为( )
在点
处的切线方程为( )
| A. |
|
B. |
|
C. |
|
D. |
|
某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
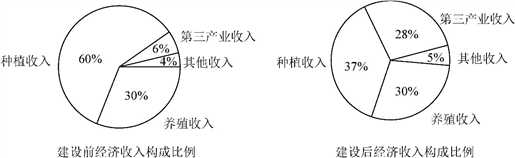
则下面结论中不正确的是( )
| A. |
新农村建设后,种植收入减少 |
| B. |
新农村建设后,其他收入增加了一倍以上 |
| C. |
新农村建设后,养殖收入增加了一倍 |
| D. |
新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 |
设函数 .
(1)当 时,求不等式 的解集;
(2)若 恒成立,求 的取值范围.
在直角坐标系 中,曲线 的参数方程为 ( 为参数),直线 的参数方程为 ( 为参数).
(1)求 和 的直角坐标方程;
(2)若曲线 截直线 所得线段的中点坐标为 ,求 的斜率.
已知函数 .
(1)若 ,证明:当 时, ;
(2)若
在 只有一个零点,求
的值.
只有一个零点,求
的值.