设
,
是双曲线  (
( 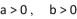 )的左、右焦点,
是坐标原点.过
作
的一条渐近线的垂线,垂足为
.若
,则
的离心率为( )
)的左、右焦点,
是坐标原点.过
作
的一条渐近线的垂线,垂足为
.若
,则
的离心率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
设 是同一个半径为4的球的球面上四点, 为等边三角形且其面积为 ,则三棱锥 体积的最大值为( )
| A. |
|
B. |
|
C. |
|
D. |
|
的内角 的对边分别为 , , ,若 的面积为 ,则 ( )
| A. |
|
B. |
|
C. |
|
D. |
|
某群体中的每位成员使用移动支付的概率都为 ,各成员的支付方式相互独立,设 为该群体的10位成员中使用移动支付的人数, , ,则 ( )
| A. |
0.7 |
B. |
0.6 |
C. |
0.4 |
D. |
0.3 |
直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积的取值范围是( )
| A. |
|
B. |
|
C. |
|
D. |
|
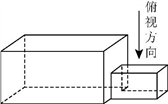
中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知函数 .
(Ⅰ)若f(x)在x=x 1,x 2(x 1≠x 2)处导数相等,证明:f(x 1)+f(x 2)>8−8ln2;
(Ⅱ)若a≤3−4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y 2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.

(Ⅰ)设AB中点为M,证明:PM垂直于y轴;
(Ⅱ)若P是半椭圆x 2+ =1(x<0)上的动点,求△PAB面积的取值范围.