能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是__________.
设集合 则( )
| A. |
对任意实数a, |
| B. |
对任意实数a,(2,1) |
| C. |
当且仅当a<0时,(2,1) |
| D. |
当且仅当 时,(2,1) |
在平面直角坐标系中,记 为点 到直线 的距离,当 、 变化时, 的最大值为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
设向量 均为单位向量,则" "是" "的( )
| A. |
充分不必要条件 |
B. |
必要不充分条件 |
C. |
充要条件 |
D. |
既不充分又不必要条件 |
某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )

| A. |
1 |
B. |
2 |
| C. |
3 |
D. |
4 |
"十二平均律" 是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 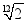 .若第一个单音的频率为 f ,则第八个单音的频率为( )
.若第一个单音的频率为 f ,则第八个单音的频率为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
在复平面内,复数 的共轭复数对应的点位于( )
| A. |
第一象限 |
B. |
第二象限 |
| C. |
第三象限 |
D. |
第四象限 |
已知集合 , ,则 ( )
| A. | {0,1} |
B. | {−1,0,1} |
| C. | {−2,0,1,2} |
D. | {−1,0,1,2} |
已知函数 , ,其中 a>1.
(I)求函数 的单调区间;
(II)若曲线 在点 处的切线与曲线 在点 处的切线平行,证明 ;
(III)证明当 时,存在直线 l,使 l是曲线 的切线,也是曲线 的切线.