)在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1、F2分别为椭圆 =1的左、右焦点.已知△F1PF2为等腰三角形.
=1的左、右焦点.已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足 =-2,求点M的轨迹方程.
=-2,求点M的轨迹方程.
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段 ,
, …
… 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩为x,y,求满足“ ”的概率.
”的概率.
已知椭圆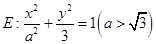 的离心率
的离心率 .直线x=t(t>0)与曲线E交于不同的两点
.直线x=t(t>0)与曲线E交于不同的两点 ,
,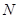 ,以线段
,以线段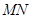 为直径作圆
为直径作圆 ,圆心为
,圆心为 .
.
(1)求椭圆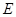 的方程;
的方程;
(2)若圆 与y轴相交于不同的两点A,B,求△ABC的面积的最大值.
与y轴相交于不同的两点A,B,求△ABC的面积的最大值.
(本小题满分12分)椭圆G  的长轴为4
的长轴为4 ,焦距为4
,焦距为4 .
.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点, 且点P(-3,2)在线段AB的垂直平分线上,求PAB的面积.
(本小题满分12分)已知双曲线 ,若双曲线的渐近线过点
,若双曲线的渐近线过点 ,且双曲线过点
,且双曲线过点
(1) 求双曲线 的方程;
的方程;
(2)若双曲线 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在
在 上且直线
上且直线 的斜率的取值范围是
的斜率的取值范围是 ,求直线
,求直线 斜率的取值范围.
斜率的取值范围.
(本小题满分12分)已知椭圆C的方程为 ,定点N(0,1),过圆M:
,定点N(0,1),过圆M: 上任意一点作圆M的一条切线交椭圆
上任意一点作圆M的一条切线交椭圆 于
于 、
、 两点.
两点.


(1)求证: ;
;
(2)求 的取值范围;
的取值范围;
(3)若点P、Q在椭圆C上,直线PQ与x轴平行,直线PN交椭圆于另一个不同的点S,问:直线QS是否经过一个定点?若是,求出这个定点的坐标;若不是,说明理由.
椭圆C: 的左、右焦点分别是F1、F2,离心率为
的左、右焦点分别是F1、F2,离心率为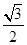 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF1、PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围.
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1、PF2的斜率分别为k1、k2,若k≠0,试证明 为定值,并求出这个定值.
为定值,并求出这个定值.
已知 为实数,函数
为实数,函数 .
.
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)定义:若函数 的图象上存在两点
的图象上存在两点 、
、 ,设线段
,设线段 的中点为
的中点为 ,若
,若 在点
在点 处的切线
处的切线 与直线
与直线 平行或重合,则函数
平行或重合,则函数 是“中值平衡函数”,切线
是“中值平衡函数”,切线 叫做函数
叫做函数 的“中值平衡切线”.试判断函数
的“中值平衡切线”.试判断函数 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数 的“中值平衡切线”的条数;若不是,说明理由;
的“中值平衡切线”的条数;若不是,说明理由;
()设 ,若存在
,若存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数 .
.
(1)判断 的奇偶性.
的奇偶性.
(2)判断 在
在 上的单调性,并用定义证明.
上的单调性,并用定义证明.
(3)是否存在实数 ,使不等式
,使不等式 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)设函数 .
.
(1)若函数 在
在 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)①是否存在实数 ,使得关于
,使得关于 的不等式
的不等式 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式
(本小题满分12分) 已知函数 .
.
(Ⅰ)函数 在
在 处的切线方程为
处的切线方程为 ,求a、b的值;
,求a、b的值;
(Ⅱ)当 时,若曲线
时,若曲线 上存在三条斜率为k的切线,求实数k的取值范围.
上存在三条斜率为k的切线,求实数k的取值范围.