已知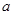 为实数,函数
为实数,函数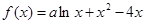 .
.
(1)当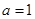 时,求
时,求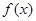 在
在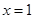 处的切线方程;
处的切线方程;
(2)定义:若函数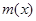 的图象上存在两点
的图象上存在两点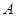 、
、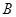 ,设线段
,设线段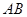 的中点为
的中点为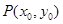 ,若
,若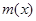 在点
在点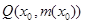 处的切线
处的切线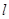 与直线
与直线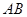 平行或重合,则函数
平行或重合,则函数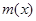 是“中值平衡函数”,切线
是“中值平衡函数”,切线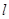 叫做函数
叫做函数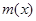 的“中值平衡切线”.试判断函数
的“中值平衡切线”.试判断函数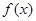 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数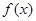 的“中值平衡切线”的条数;若不是,说明理由;
的“中值平衡切线”的条数;若不是,说明理由;
()设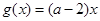 ,若存在
,若存在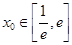 ,使得
,使得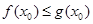 成立,求实数
成立,求实数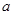 的取值范围.
的取值范围.
推荐套卷
已知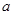 为实数,函数
为实数,函数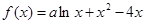 .
.
(1)当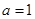 时,求
时,求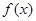 在
在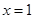 处的切线方程;
处的切线方程;
(2)定义:若函数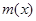 的图象上存在两点
的图象上存在两点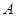 、
、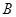 ,设线段
,设线段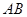 的中点为
的中点为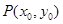 ,若
,若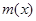 在点
在点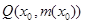 处的切线
处的切线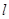 与直线
与直线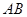 平行或重合,则函数
平行或重合,则函数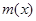 是“中值平衡函数”,切线
是“中值平衡函数”,切线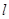 叫做函数
叫做函数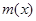 的“中值平衡切线”.试判断函数
的“中值平衡切线”.试判断函数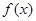 是否是“中值平衡函数”?若是,判断函数
是否是“中值平衡函数”?若是,判断函数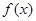 的“中值平衡切线”的条数;若不是,说明理由;
的“中值平衡切线”的条数;若不是,说明理由;
()设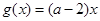 ,若存在
,若存在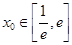 ,使得
,使得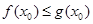 成立,求实数
成立,求实数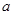 的取值范围.
的取值范围.