如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
(1)求证:PE⊥BC;
(2)求证:EF∥平面PAD.
已知函数 在
在 上有最大值1和最小值0,设
上有最大值1和最小值0,设 (
(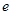
为自然对数的底数).
(1)求 的值;
的值;
(2)若不等式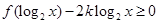 在
在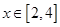 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
已知数列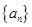 为等差数列,
为等差数列,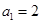 ,
,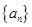 的前
的前 和为
和为 ,数列
,数列 为等
为等
比数列,且 对任意的
对任意的 恒成立.
恒成立.
(Ⅰ)求数列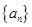 、
、 的通项公式;
的通项公式;
(Ⅱ)是否存在非零整数 ,使不等式
,使不等式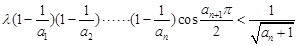 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)各项均为正整数的无穷等差数列 ,满足
,满足 ,且存在正整数k,使
,且存在正整数k,使 成等比数列,若数列
成等比数列,若数列 的公差为d,求d的所有可能取值之和.
的公差为d,求d的所有可能取值之和.
如图, 中,
中, 是
是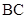 的中点,
的中点, ,
, .将
.将 沿
沿 折起,使
折起,使 点与图中
点与图中 点重合.
点重合.
(1)求证: 平面
平面 ;
;
(2)当三棱锥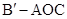 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(3)在(2)条件下,试问在线段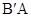 上是否存在一点
上是否存在一点 ,使
,使 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?证明你的结论.
?证明你的结论.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.

(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(下面的临界值表供参考)
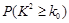 |
0.10 |
0.05 |
0.010 |
0.005 |
 |
2.706 |
3.841 |
6.635 |
7.879 |
(2)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,
求3名幸运选手中至少有一人在20~30岁之间的概率.
(参考公式: .其中
.其中 .)
.)
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.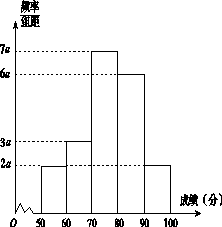
(1)求频率分布直方图中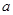 的值;
的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数.
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
 (月) (月) |
 |
 |
 |
 |
 |
 (千克) (千克) |
 |
 |
 |
 |
 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.

(2)请根据上表提供的数据,用最小二乘法求出变量 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: ,
, ,
, ,
, ,
, ,
,
如图所示,椭圆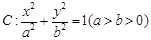 与直线
与直线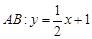 相切于点
相切于点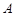 .
.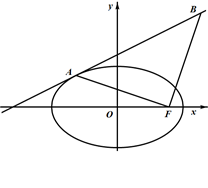
(1)求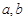 满足的关系式,并用
满足的关系式,并用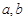 表示点
表示点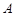 的坐标;
的坐标;
(2)设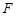 是椭圆的右焦点,若
是椭圆的右焦点,若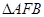 是以
是以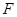 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆 的标准方程.
的标准方程.
已知椭圆 的右焦点为
的右焦点为 ,
, 为短轴的一个端点,且
为短轴的一个端点,且 ,
, 的面积为1(其中
的面积为1(其中 为坐标原点).
为坐标原点).
(1)求椭圆的方程;
(2)若 ,
, 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点 ,证明:
,证明: 为定值.
为定值.