(本小题满分14分)
设数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
(Ⅰ)若 成等比数列,试求
成等比数列,试求 的值;
的值;
(Ⅱ)是否存在 ,使得数列
,使得数列 中存在某项
中存在某项 满足
满足 成等差数列?若存在,请指出符合题意的
成等差数列?若存在,请指出符合题意的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
21.(本小题满分14分)
已知数列 满足:
满足: .
.
(Ⅰ)问数列 是否为等差数列或等比数列?说明理由;
是否为等差数列或等比数列?说明理由;
(Ⅱ)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
20.(本小题满分14分)
已知圆 和椭圆
和椭圆
 的一个公共点为
的一个公共点为 .
. 为椭圆
为椭圆 的右焦点,直线
的右焦点,直线 与圆
与圆 相切于点
相切于点 .
.
(Ⅰ)求 值和椭圆
值和椭圆 的方程;
的方程;
(Ⅱ)圆 上是否存在点
上是否存在点 ,使
,使 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点 的坐标.
的坐标.
19.(本小题满分13分)
已知函数 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求函数 的图象在
的图象在 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在区间
在区间 上的最大值与最小值.
上的最大值与最小值.
21.(本小题满分14分)
设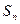 是数列
是数列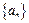 的前
的前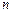 项和,且
项和,且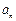 是
是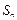 和
和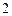 的等差中项.
的等差中项.
(1)求数列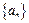 的通项公式;
的通项公式;
(2)当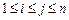 (
(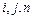 均为正整数)时,求
均为正整数)时,求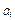 和
和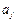 的所有可能的乘积
的所有可能的乘积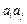 之和
之和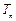 ;
;
(3)设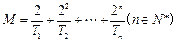 ,求证:
,求证: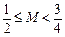 .
.
20.(本小题满分14分)
已知抛物线 :
: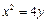 的焦点为
的焦点为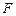 ,过点
,过点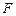 作直线
作直线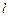 交抛物线
交抛物线 于
于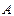 、
、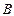 两点;椭圆
两点;椭圆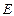 的中心在原点,焦点在
的中心在原点,焦点在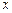 轴上,点
轴上,点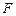 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率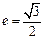 .
.
(1)求椭圆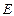 的方程;
的方程;
(2)经过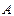 、
、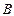 两点分别作抛物线
两点分别作抛物线 的切线
的切线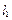 、
、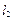 ,切线
,切线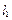 与
与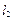 相交于点
相交于点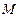 .证明:
.证明: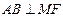 ;
;
(3)椭圆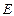 上是否存在一点
上是否存在一点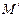 ,经过点
,经过点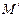 作抛物线
作抛物线 的两条切线
的两条切线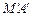 、
、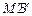 (
(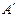 、
、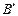 为切点),使得直线
为切点),使得直线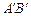 过点
过点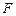 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线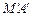 、
、 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
 |
19.(本小题满分14分)
设函数 (
( ,
, ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时 的值,并证明你的结论.
的值,并证明你的结论.
18.(本小题满分14分)
如图5,四边形 是圆柱
是圆柱 的轴截面,点
的轴截面,点 在圆柱
在圆柱 的底面圆周上,
的底面圆周上, 是
是 的中点,圆柱
的中点,圆柱 的底面圆的半径
的底面圆的半径 ,侧面积为
,侧面积为 ,
, .
.
(1)求证: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
17.(本小题满分12分)
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示.
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(图4),再根据频率分布直方图估计这507个画师中年龄在 岁的人数(结果取整数);
岁的人数(结果取整数);
(2)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动,其中选取2名画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为ξ,求ξ的分布列及数学期望.
| 分组 (单位:岁) |
频数 |
频率 |
 |
5 |
0.050 |
 |
① |
0.200 |
 |
35 |
② |
 |
30 |
0.300 |
 |
10 |
0.100 |
| 合计 |
100 |
1.00 |

已知 其中
其中 是自然常数,
是自然常数,
(1)讨论 时,
时, 
 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下,
(3)是否存在实数 ,使
,使 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30 ,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.若△OE F的面积不小于2
F的面积不小于2 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面A BCD,O是BC中点,AO交BD于E.
BCD,O是BC中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB.
今天你低碳了吗?近来,国内网站流行一种名为“碳排放计算器”的软件,人们可以扰此计算出自己每天的碳排放量。例如:家居用电的碳排放量(千克)=耗电度数×0.785,汽车的碳排放量(千克)=油耗公升数×0.785等。某班同学利用寒假在两个小区逐户进行了一次生活习惯进否符合低碳观 念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如下:
念的调查。若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”。这二族人数占各自小区总人数的比例P数据如下:
|
|
||||||||||||||||
 甲、乙来自A小区,丙、丁来自B小区,求这4人中恰有2人是低碳族的概率;
甲、乙来自A小区,丙、丁来自B小区,求这4人中恰有2人是低碳族的概率;
 表示25个人中低碳族人数,求
表示25个人中低碳族人数,求
