如图，在以点O为圆心，|AB|=4为直径的半圆ADB中，OD⊥AB，P是半圆弧上一点，∠POB=30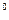
，曲线C是满足||MA|－|MB||为定值的动点M的轨迹，且曲线C过点P．
（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；
（Ⅱ）设过点D的直线l与曲线C相交于不同的两点E、F．若△OE
F的面积不小于2
，求直线l斜率的取值范围．
，且
．
。
时，求函数
的最小值；
时，试判断函数
的周长为
，且
．
的值；
（结果用反三角函数值表示）．
.
的值域G；
，不等式
恒成立，求实数
的取值范围.推荐套卷
如图，在以点O为圆心，|AB|=4为直径的半圆ADB中，OD⊥AB，P是半圆弧上一点，∠POB=30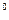，曲线C是满足||MA|－|MB||为定值的动点M的轨迹，且曲线C过点P．
（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；
（Ⅱ）设过点D的直线l与曲线C相交于不同的两点E、F．若△OEF的面积不小于2，求直线l斜率的取值范围．
粤公网安备 44130202000953号