高中数学解答题

设{a_n}是公比为q的等比数列．
（Ⅰ）推导{a_n}的前n项和S_n公式；
（Ⅱ）设q≠1，证明数列不是等比数列．

在△ABC中，已知2sinBcosA=sin（A+C）．
（Ⅰ）求角A；
（Ⅱ）若BC=2，△ABC的面积是，求AB．

已知函数f（x）=x²+ax+6．
（1）当a=5时，解不等式f（x）＜0；
（2）若不等式f（x）＞0的解集为R，求实数a的取值范围．

已知函数f（x）=（ax²﹣2x+a）e^﹣x
（Ⅰ）当a=1时，求函数f（x）的单调区间；
（Ⅱ）设，若x＞l时总有g（x）＜h（x），求实数c范围．

如图，椭圆C：+=1（a＞b＞0）的右焦点为F，右顶点、上顶点分别为点A、B，且|AB|=|BF|．

（Ⅰ）求椭圆C的离心率；
（Ⅱ）若斜率为2的直线l过点（0，2），且l交椭圆C于P、Q两点，OP⊥OQ．求直线l的方程及椭圆C的方程．

（Ⅰ）求右焦点坐标是（2，0），且经过点的椭圆的标准方程
（Ⅱ）求与椭圆共焦点且过点的双曲线的标准方程．

已知函数是偶函数．
（1）求k的值；
（2）若函数y=f（x）的图象与直线没有交点，求b的取值范围．
（3）设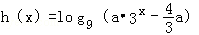，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．
（Ⅰ）当每辆车的月租金定为3600元时，能租出多少辆车？
（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

已知函数f（x）=．
（1）求函数f（x）的定义域；
（2）判断函数f（x）的奇偶性，并说明理由．

定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M 成立，则称f（x）是D上的有界函数，其中M称为函f（x）的一个上界．已知函数f（x）=1+a+，g（x）=．
（1）若函数g（x）为奇函数，求实数a的值；
（2）在（1）的条件下，求函数g（x），在区间[，3]上的所有上界构成的集合；
（3）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．

已知幂函数f（x）=x^﹣m2+m+2（m∈Z）在（0，+∞）上单调递增．
（1）求函数f（x）的解析式；
（2）设g（x）=f（x）﹣ax+1，a为实常数，求g（x）在区间[﹣1，1]上的最小值．

已知函数f（x）=log₄（4^x+1）+kx（k∈R）是偶函数．
（1）求实数k的值；
（2）设g（x）=log₄（a•2^x+a），若f（x）=g（x）有且只有一个实数解，求实数a的取值范围．

已知函数f（x）=a^|x+b|（a＞0，a≠1，b∈R）．
（1）若f（x）为偶函数，求b的值；
（2）若f（x）在区间[2，+∞）上是增函数，试求a、b应满足的条件．

已知函数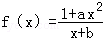（a≠0）是奇函数，并且函数f（x）的图象经过点（1，3），
（1）求实数a，b的值；
（2）求函数f（x）的值域．

记函数f（x）=log₂（2x﹣3）的定义域为集合M，函数g（x）=的定义域为集合N．求：
（1）集合M，N；
（2）集合M∩N，∁_R（M∪N）．