某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测20人,得到如下数据:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 身高x(厘米) |
192 |
164 |
172 |
177 |
176 |
159 |
171 |
166 |
182 |
166 |
| 脚长y(码) |
48 |
38 |
40 |
43 |
44 |
37 |
40 |
39 |
46 |
39 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 身高x(厘米) |
169 |
178 |
167 |
174 |
168 |
179 |
165 |
170 |
162 |
170 |
| 脚长y(码) |
43 |
41 |
40 |
43 |
40 |
44 |
38 |
42 |
39 |
41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的 列联表:
列联表:
| |
高个 |
非高个 |
合计 |
| 大脚 |
|
|
|
| 非大脚 |
|
12 |
|
| 合计 |
|
|
20 |
(2)根据(1)中表格数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
附: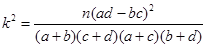
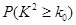 |
0.050 |
0.010 |
0.001 |
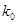 |
3.841 |
6.635 |
10.828 |
已知椭圆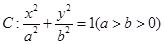 中,椭圆长轴长是短轴长的
中,椭圆长轴长是短轴长的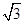 倍,短轴的一个端点与两个焦点构成的三角形的面积为
倍,短轴的一个端点与两个焦点构成的三角形的面积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知动直线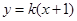 与椭圆
与椭圆 相交于
相交于 两点,
两点,
①若线段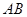 的中点的横坐标为
的中点的横坐标为 ,求斜率
,求斜率 的值;
的值;
②已知点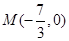 ,求证:
,求证: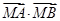 为定值.
为定值.
我市在夜明珠与黄柏河交汇形成的平湖水面上修建”三峡游轮中心”.其中有小型游艇出租给游客游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为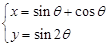 (
(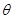 为参数),若以该直角坐标系的原点
为参数),若以该直角坐标系的原点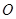 为极点,
为极点,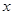 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为:
的极坐标方程为: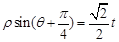 (其中
(其中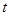 为常数).
为常数).
(Ⅰ)若曲线 与曲线
与曲线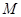 只有一个公共点,求
只有一个公共点,求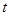 的取值范围;
的取值范围;
(Ⅱ)当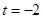 时,求曲线
时,求曲线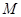 上的点与曲线
上的点与曲线 上点的最小距离.
上点的最小距离.
 为等腰直角三角形,
为等腰直角三角形, ,
, ,
, 、
、 分别是边
分别是边 和
和 的中点,现将
的中点,现将 沿
沿 折起,使面
折起,使面
 面
面 ,
, 、
、 分别是边
分别是边 和
和 的中点,平面
的中点,平面 与
与 、
、 分别交于
分别交于 、
、 两点.
两点.
(Ⅰ)求证:

 ;
;
(Ⅱ)求二面角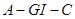 的余弦值;
的余弦值;