高中数学解答题

已知f（x）=（n∈Z）．
（1）化简f（x）的表达式；      
（2）求f（）+f（π）．

李庄村电费收取有以下两种方案供农户选择：
方案一：每户每月收管理费2元，月用电不超过30度每度0.5元，超过30度时，超过部分按每度0.6元．
方案二：不收管理费，每度0.58元．
（1）求方案一收费L（x）元与用电量x（度）间的函数关系；
（2）李刚家九月份按方案一交费35元，问李刚家该月用电多少度？
（3）李刚家月用电量在什么范围时，选择方案一比选择方案二更好？

在平面直角坐标系xOy中，已知向量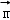=（，﹣），=（sinx，cosx），x∈（0，）．
（1）若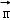⊥，求tanx的值；
（2）若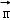与的夹角为，求sinx+cosx的值．

已知方程x²+px+q=0的两个不相等实根为α，β．集合A={α，β}，B={2，4，5，6}，C={1，2，3，4}，A∩C=A，A∩B=∅，求p，q的值？

如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．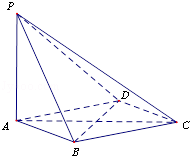

（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）当平面PBC与平面PDC垂直时，求PA的长．

已知三角形ABC的三个顶点A（1，1），B（4，0），C（3，2），求三角形BC边上的高线和中线所在的直线方程．

已知f（α）=．
（1）化简f（α）；
（2）若角α终边上一点的坐标为（5a，12a），a≠0，求f（α）的值．

已知，0＜β＜，cos（+α）=﹣，sin（+β）=，求sin（α+β）的值．

某批发市场对某种商品的日销售量（单位：吨）进行统计，最近50天的结果如下：

日销售量	1	1.5	2
频数	10	25	15
频率	0.2	a	b

 
（1）求表中a，b的值
（2）若以上表频率作为概率，且每天的销售量相互独立，
①求5天中该种商品恰有2天销售量为1.5吨的概率；
②已知每吨该商品的销售利润为2千元，X表示该种商品两天销售利润的和（单位：千元），求X的分布列和期望．

已知圆心C（1，2），且经过点（0，1）
（Ⅰ）写出圆C的标准方程；
（Ⅱ）过点P（2，﹣1）作圆C的切线，求切线的方程及切线的长．

已知在（+）ⁿ的展开式中，只有第6项的二项式系数最大．
（1）求n； 
（2）求展开式中含x⁴项．

设命题p：（4x﹣3）²≤1；命题q：x²﹣（2a+1）x+a（a+1）≤0，若￢p是￢q的必要不充分条件，求实数a的取值范围．

已知f（x）=kx+b的图象过点（2，1），且b²﹣6b+9≤0
（1）求函数f（x）的解析式；
（2）若a＞0，解关于x的不等式x²﹣（a²+a+1）x+a³+3＜f（x）．

在△ABC中，角A，B，C所对的边分别为a，b，c，且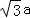=2csinA．
（1）求角C的大小；
（2）若△ABC为锐角三角形，且c=2，且a+b=3，求△ABC的面积．

已知集合，，是否存在实数，使?若存在，求实数的取值范围；若不存在，请说明理由．