我市在夜明珠与黄柏河交汇形成的平湖水面上修建”三峡游轮中心”.其中有小型游艇出租给游客游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
相关知识点
推荐套卷
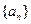 的前
的前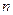 项和为
项和为 ,且
,且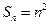 .数列
.数列 为等比数列,且
为等比数列,且 ,
,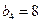 .
.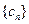 满足
满足 ,求数列
,求数列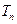 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号