本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为
,
;两小时以上且不超过三小时还车的概率分别为
,
;两人租车时间都不会超过四小时.
(Ⅰ)求出甲、乙所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量
,求
的分布列与数学期望
.
相关知识点
推荐套卷
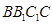 是矩形,
是矩形, 平面
平面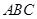 ,
,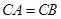 ,
,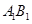 ∥
∥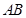 ,
, ,
,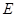 ,
,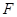 分别是
分别是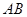 ,
,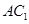 的中点.
的中点.
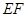 ∥平面
∥平面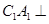 平面
平面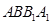 .
.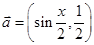 ,
, ,函数
,函数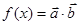 ,
,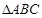 三个内角
三个内角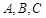 的对边分别为
的对边分别为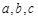 .
.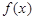 的单调递增区间;
的单调递增区间;
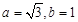 ,求
,求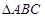 的面积
的面积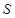 .
. .
.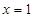 是函数
是函数 的极值点,求
的极值点,求 的值并讨论
的值并讨论 时,证明:
时,证明: .
. :
: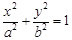 (
( )的焦距为
)的焦距为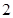 ,且过点(
,且过点( ,
, ),右焦点为
),右焦点为 .设
.设 ,
, 是
是 的中点
的中点 的横坐标为
的横坐标为 ,线段
,线段 ,
, 两点.
两点.
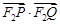 的取值范围.
的取值范围. 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点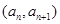 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数. 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列; ,
, ,求
,求 ;
; ,求数列
,求数列 的前
的前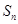 ,并求使
,并求使 的
的 粤公网安备 44130202000953号
粤公网安备 44130202000953号