高中数学解答题

二次函数满足且．
（1）求的解析式；
（2）求在区间上的最大值与最小值．

已知圆与圆相切于点，求以为圆心，且与圆的半径相等的圆的标准方程．

在四棱锥中，底面为矩形，侧棱底面，且，过棱的中点，作交于点，连接

（Ⅰ）证明：；
（Ⅱ）求异面直线与所成角的余弦值及二面角的余弦值．

设条件：实数满足；条件：实数满足且命题“若，则”的逆否命题为真命题，求实数的取值范围．

要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示：

规格类型 钢板规格	A规格	B规格	C规格
第一种钢板	2	1	1
第二种钢板	1	2	3

 
今需A、B、C三种规格的成品分别为15、18、27块，问各截这两种钢板多少张可得所需A、B、C三种规格成品，且使所用的钢板的张数最少？

已知等差数列{a_n}的前n项和为S_n，S₅＝35，a₅和a₇的等差中项为13．
（1）求a_n及S_n；
（2）令b_n＝（n∈N^*），求数列{b_n}的前n项和T_n．

设，
（1）若，求的值；
（2）求的值．

若集合，且，求实数的取值集合．

证明“0≤a≤”是“函数f（x）＝ax²＋2（a－1）x＋2在区间（－∞，4]上为减函数”的充分不必要条件．

在△ABC中，内角A、B、C对边的边长分别是a、b、c．已知c=2，．
（1）若△ABC的面积等于求a与b的值；
（2）若sinB=2sinA，求△ABC的面积．

已知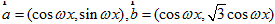，其中0＜ω＜2．函数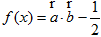，其图象的一条对称轴为x＝．
（1）求函数f（x）的表达式及单调递增区间；
（2）在△ABC中，a，b，c分别为角A，B，C的对边，S为其面积，若，b＝1，S_△ABC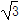＝，求a的值．

在△中，内角、、的对边分别是、、，且．
（Ⅰ）求；
（Ⅱ）设，，求的值．

递增等比数列{a_n}满足a₂＋a₃＋a₄＝28，且a₃＋2是a₂和a₄的等差中项．
（1）求数列{a_n}的通项公式；
（2）若，求数列{b_n}的前n项和．

从高三抽出50名学生参加数学竞赛，由成绩得到如下的频率分布直方图．由于一些数据丢失，试利用频率分布直方图求：

（1）这50名学生成绩的众数与中位数．
（2）这50名学生的平均成绩．

计算：
（Ⅰ）；
（Ⅱ）