(本小题满分12分)已知函数f(x)=  (a,b为常数,且a≠0)满足f(2)= 1且方程f(x)= x有唯一解 ,求函数f(x)的解析式
(a,b为常数,且a≠0)满足f(2)= 1且方程f(x)= x有唯一解 ,求函数f(x)的解析式
本小题满分12分)某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y( 件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
把角各截去一个边长为x的小正方形,然后焊接成一个无盖的蓄水池。
(Ⅰ)写出以x为自变量的容积V的函数解析式V(x),并求函数V(x)的定义域;
(Ⅱ)指出函数V(x)的单调区间;
(Ⅲ)蓄水池的底边为多少时,蓄水池的容积最大?最大容积是多少?
(1)在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求a的值;
(2)设矩阵 ,求点P(2,2)在A所对应的线性变换下的象。
,求点P(2,2)在A所对应的线性变换下的象。
(本小题满分13分)
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;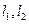 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,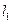 交E于A,B两点,
交E于A,B两点,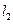 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求 k的取值范围;
k的取值范围;
(3)求证直线OM与直线ON的斜率乘积为定值(O为坐标原点)
(本小题满分13分)
已知函数 为自然对数的底数,
为自然对数的底数,
(1)求 的单调区间,若
的单调区间,若 有最值,请求出最值;
有最值,请求出最值;
(2)当 图象的一个公共点坐标,并求它们在该公共点处的切线方程。
图象的一个公共点坐标,并求它们在该公共点处的切线方程。
(本小题满分12分)
在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE//平面ABC,平面ACD⊥平面ABC。
(1)求证:DE⊥平面ACD;
(2)若AB=BE=2,求多面体ABCDE的体积。
(本小题满分12分)
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名学生进行调查,下表是这n名学生的日睡眠时间的频率分布表。
| 序号(i) |
分组(睡眠时间) |
频数(人数) |
频率 |
| 1 |
[4,5) |
6 |
0.12 |
| 2 |
[5,6) |
|
0.20 |
| 3 |
[6,7) |
a |
|
| 4 |
[7,8) |
b |
|
| 5 |
[8,9) |
|
0.08 |
(1)求n的值.若 ,将表中数据补全,并画出频率分布直方图.
,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求
的中点值是5)作为代表.若据此计算的上述数据的平均值为7.2,求 的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.
的值,并由此估计该学校学生的日平均睡眠时间在7.5小时以上的概率.