高中数学解答题

如图，正四棱柱中，，点在上且
(1)证明：平面；
(2)求二面角的余弦值．

(12分)若集合A＝{x|x²－2x－8<0}，B＝{x|x－m<0}．
(1)若m＝3，全集U＝A∪B，试求；
(2)若A∩B＝∅，求实数m的取值范围；
(3)若A∩B＝A，求实数m的取值范围．

(12分)已知p：x²－8x－20≤0，q：x²－2x＋1－m²≤0(m>0)，且非p是非q的必要不充分条件，求实数m的取值范围．

(12分)(2010·徐州模拟)已知f(x)＝x²－2x＋1，g(x)是一次函数，且f[g(x)]＝4x²，求g(x)的解析式．

（本小题满分14分）已知，若函数在区间上
的最大值为，最小值为，令.
（1）求的函数表达式；
（2）判断函数在区间上的单调性，并求出的最小值.

（本小题满分14分）已知直线:y=k(x+2)与圆O：x²+y²=4相交于不重合的
A、B两点，O是坐标原点，且三点A、B、O构成三角形．
（1）求k的取值范围；
（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；
（3）求S的最大值，并求取得最大值时k的值．

（本小题满分12分）在一个选拔项目中，每个选手都需要进行4轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为、、、，且各轮问题能否正确回答互不影响。
（Ⅰ）求该选手进入第三轮才被淘汰的概率；
（Ⅱ）求该选手至多进入第三轮考核的概率；

已知p: ,q: ,若是的必要不
充分条件，求实数m的取值范围。

（本小题满分12分）已知函数，且。
（1）求的值；
（2）判定的奇偶性；
（3）判断在上的单调性，并给予证明。

.(本小题满分12分)
已知以函数f(x)＝mx³－x的图象上一点N(1，n)为切点的切线倾斜角为.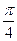
(1)求m、n的值；
(2)是否存在最小的正整数k，使得不等式f(x)≤k－1995，对于x∈[－1,3]恒成立？若存在，求出最小的正整数k，否则请说明理由．

已知函数f(x)＝Asin(ωx＋φ)＋B(A＞0，ω＞0)的一系列对应值如下表：
 (1)根据表格提供的数据求函数f(x)的一个解析式；
(2)根据(1)的结果，若函数y＝f(kx)(k＞0)周期为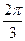，当x∈[0，]时，方程f(kx)＝m
恰有两个不同的解，求实数m的取值范围；

已知函数，
(Ⅰ)求的最小正周期和最大值；
(Ⅱ) 求的单调递增区间。

求函数在闭区间上的最大值？

已知，
求的值。

（本小题14分）已知函数的图像与函数的图像关于点
对称
（1）求函数的解析式；
（2）若，在区间上的值不小于6，求实数a的取值范围．