（本小题满分14分）已知直线
:y=k(x+2
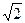)与圆O：x2+y2=4相交于不重合的
A、B两点，O是坐标原点，且三点A、B、O构成三角形．
（1）求k的取值范围；
（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；
（3）求S的最大值，并求取得最大值时k的值．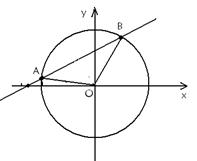
相关试题
是等差数列，
是各项为正数的等比数列，且
，
，
. 
，求数列
的前
项和
.
和直线
相切，且圆心在直线
上的圆的方程。
中，
，
点
是
的中点。
与平面
所成的角的正切值
，直线
截得的弦长何时最短？并求截得的弦长最短时
的值及最短长度。
，B=
．
，求实数
的取值范围；
，求实数推荐套卷
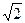（本小题满分14分）已知直线:y=k(x+2)与圆O：x2+y2=4相交于不重合的
A、B两点，O是坐标原点，且三点A、B、O构成三角形．
（1）求k的取值范围；
（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；
（3）求S的最大值，并求取得最大值时k的值．
粤公网安备 44130202000953号