[江西]2012届江西省六校高三第一次联考理科数学
如果对于任意实数 ,
, 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,那么“
,那么“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2012届江西省六校高三第一次联考理科数学
若自然数n使得作竖式加法 均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )
均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1000的“良数”的个数为 ( )
| A.27 | B.36 | C.39 | D.48 |
来源:2012届江西省六校高三第一次联考理科数学
如图,一个树形图依据下列规律不断生长:1个空心圆
点到下一行仅生长出1个实心圆点,1个实心圆点到下
一行生长出1个实心圆点和1个空心圆点.则第11行
的实心圆点的个数是

来源:2012届江西省六校高三第一次联考理科数学
车站每天8∶00~9∶00,9∶00~10∶00都恰有一辆客车到站,8∶00~9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00~10∶00到站的客车B可能在9∶10,9∶30,
;9∶00~10∶00到站的客车B可能在9∶10,9∶30, 9∶50到站,其概率依次为
9∶50到站,其概率依次为 .
.
(1)旅客甲8∶00到站,设他的候车时间为 ,求
,求 的分布列和
的分布列和 ;
;
(2)旅客乙8∶20到站,设他的候车时间为 ,求
,求 的分布列和
的分布列和 .
.
来源:2012届江西省六校高三第一次联考理科数学
已知定义在(0,+ )上的函数
)上的函数 是增函数
是增函数
(1)求常数 的取值范围
的取值范围
(2)过点(1,0)的直线与 (
( )的图象有交点,求该直线的斜率的取值范围
)的图象有交点,求该直线的斜率的取值范围
来源:2012届江西省六校高三第一次联考理科数学
已知抛物线 的准线为
的准线为 ,焦点为
,焦点为 ,圆
,圆 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,过原点
轴相切,过原点 作倾斜角为
作倾斜角为 的直线
的直线 ,交
,交
 于点
于点 ,交圆
,交圆 于另一点
于另一点 ,且
,且
(1)求圆 和抛物线C的方程;
和抛物线C的方程;
(2)若 为抛物线C上的动点,求
为抛物线C上的动点,求 的最小值;
的最小值;
(3)过 上的动点Q向圆
上的动点Q向圆 作切线,切点为S,T,
作切线,切点为S,T,
求证:直线ST 恒过一个定点,并求该定点的坐标.
恒过一个定点,并求该定点的坐标.
来源:2012届江西省六校高三第一次联考理科数学
 为纯虚数,则
为纯虚数,则 的值为( )
的值为( )


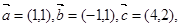 则
则 等于( )
等于( )

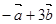
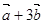
 是公比为
是公比为 的等比数列,
的等比数列, ,令
,令 ,若数列
,若数列 有连续四项在集合
有连续四项在集合 中,则
中,则








 5
5
 、
、 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为7,则
的最大值为7,则 的最小值为( )
的最小值为( ) 的图象如
的图象如 图所示,则函数
图所示,则函数



 的图像与函数
的图像与函数 的图像所有交点的横坐标之和等于
的图像所有交点的横坐标之和等于  ( )
( )


 的解集是
的解集是  的离心率为
的离心率为 ,若直线
,若直线 与其一个交点的横坐标为
与其一个交点的横坐标为 ,则
,则 的值为
的值为  线
线 ,直线
,直线 及
及 轴所围成的图形的面
轴所围成的图形的面 积为
积为  ,集合
,集合 ,且
,且 ,定义
,定义 与
与 的距离为
的距离为 ,则
,则 的概率为
的概率为  ,
, ,函数
,函数 .
. 的单调递增区间
的单调递增区间 中,
中, 分别是角
分别是角 、
、 、
、 的对边,
的对边, 且
且 ,求
,求 的最大值
的最大值 中,
中, ,点
,点 在
在
 上且
上且
 平面
平面 ;
; 的余弦值.
的余弦值.
 (
( )(
)( 为自然对数的底数)
为自然对数的底数) 的极值
的极值 ,
, (
( )
)

 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由 粤公网安备 44130202000953号
粤公网安备 44130202000953号