(本题满分13分) 已知函数 ,
, .
.
(1)当 时,若
时,若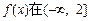 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对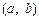 :存在
:存在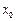 ,使得
,使得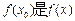 的最大值,
的最大值,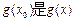 的最小值;
的最小值;
(本小题满分12分),(Ⅰ)小问5分,(Ⅱ)小问7分)
设 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3 +3
+3 -3
-3 =4
=4 bc .
bc .
(Ⅰ) 求sinA的值;
(Ⅱ)求 的值.
的值.
(本小题满分12分), (Ⅰ)小问5分,(Ⅱ)小问7分.)
已知函数 (其中常数a,b∈R),
(其中常数a,b∈R), 是奇函数.
是奇函数.
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 在区间上的最大值和最小值.
在区间上的最大值和最小值.
(本小题满分12分)
设二次函数 满足下列条件:①当
满足下列条件:①当 时,
时, 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线 对称;②当
对称;②当 时,
时, 恒成立.
恒成立.
(1)求 的值
的值
(2)求 的解析式;
的解析式;
(3)若 在区间
在区间 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.
(本题12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
如图,四边形 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又 =1,
=1,
∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(本小题满分14分)如图所示,椭圆 的离心率为
的离心率为 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线 距离的最小值。
距离的最小值。
(满分12分)已知圆C的方程为:
(1)若圆C的切线l在x轴和y轴上的截距相等,求切线l的方程;
(2)过原点的直线m与圆C相交于A、B两点,若|AB|=2,求直线m的方程.