随着社会的发展,汽车逐步成为人们的代步工具,家庭轿车的保有量逐年上升,交通堵塞现象时有发生,据调查某公路段在某时段内的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度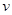 (千米/小时)之间有函数关系:
(千米/小时)之间有函数关系: .
.
(1)在该时段内,当汽车的平均速度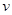 为多少时车流量
为多少时车流量 最大?最大车流量为多少?;
最大?最大车流量为多少?;
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
| 尺寸 |
 |
 |
 |
 |
 |
 |
| 甲零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
| 乙零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面
ABCD,AE⊥BD,CB=CD=CF=1,
(1)求证:BD⊥平面AED;
(2)求B到平面FDC的距离.