【原创】(本小题满分12分)已知函数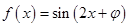 (
(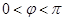 )的图象过点
)的图象过点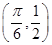 .
.
(1)求函数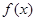 的解析式;
的解析式;
(2)若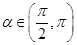 ,
, ,求
,求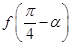 的值.
的值.
(本小题满分12分)在如图所示的几何体中, 与
与 都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形,
都是边长为2的等比三角形且所在平面互相平行,四边形BCED为正方形, ,O,G分别是BC,DE的中点.
,O,G分别是BC,DE的中点.
(1)证明:平面ADE 平面AOFG;
平面AOFG;
(2)求二面角D-AE-F的余弦值.
(本小题满分13分)某校书法兴趣组有 名男同学
名男同学 ,
, ,
, 和
和 名女同学
名女同学 ,
, ,
, ,其年级情况如下表:
,其年级情况如下表:
| |
一年级 |
二年级 |
三年级 |
| 男同学 |
 |
 |
 |
| 女同学 |
 |
 |
 |
现从这 名同学中随机选出
名同学中随机选出 人参加书法比赛(每人被选到的可能性相同).
人参加书法比赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设 为事件“选出的
为事件“选出的 人来自不同年级且性别相同”,求事件
人来自不同年级且性别相同”,求事件 发生的概率.
发生的概率.
如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧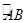 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线 与
与 所成的角为
所成的角为 ,求此圆锥的表面积.
,求此圆锥的表面积.
已知四边形 满足
满足 ,
, ,
, 是
是 的中点,将
的中点,将 沿着
沿着 翻折成
翻折成 ,使面
,使面 面
面 ,
, 分别为
分别为
 的中点.
的中点. 

(1)求三棱锥 的体积;
的体积;
(2)证明: ∥平面
∥平面 ;
;
(3)证明:平面 平面
平面
(本小题满分14分)如图,在 平面上,点
平面上,点 ,点
,点 在单位圆上,
在单位圆上, (
( )
)
(1)若点 ,求
,求 的值;
的值;
(2)若 ,
, ,求
,求 .
.
(选修4-1:几何证明选讲)
如图,AD是∠BAC的平分线,圆O过点A且与边BC相切于点D,与边AB、AC分别交于点E、F,求证:EF∥BC.
(本小题满分16分)
已知数列 是等差数列,
是等差数列, 是等比数列,且满足
是等比数列,且满足 ,
, .
.
(1)若 ,
, .
.
①当 时,求数列
时,求数列 和
和 的通项公式;
的通项公式;
②若数列 是唯一的,求
是唯一的,求 的值;
的值;
(2)若 ,
, ,
, 均为正整数,且成等比数列,求数列
均为正整数,且成等比数列,求数列 的公差
的公差 的最大值.
的最大值.
(本小题满分14分)已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, (
( ).
).
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在整数对 ,使得等式
,使得等式 成立?若存在,请求出所有满足条件的
成立?若存在,请求出所有满足条件的 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分12分)在 中,已知
中,已知 ,
, .
.
(1)求 与
与 的值;
的值;
(2)若角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,求
,求 ,
, 的值.
的值.
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设 ,
, ,
, ,求
,求 的值.
的值.
某学校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段 ,
, , ,
, , 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.