(原创)设 、
、 .
.
(1)若 在
在 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(2)若 对一切
对一切 恒成立,求证:
恒成立,求证: ;
;
(3)若对一切 ,有
,有 ,且
,且 的最大值为1,求
的最大值为1,求 、
、 满足的条件.
满足的条件.
已知椭圆 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知 为椭圆
为椭圆 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
(本小题满分13分)已知数列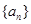 满足
满足 ,
, 为其前
为其前 项和,且
项和,且 .
.
(1)求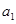 的值;
的值;
(2)求证: ;
;
(3)判断数列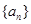 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
(本小题满分12分)如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点 和下底面的对角线
和下底面的对角线 将木块锯开,得到截面
将木块锯开,得到截面 .
.
(1)请在木块的上表面作出过 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形时矩形 ,试证明:平面
,试证明:平面 平面
平面 .
.
(本小题满分12分) 某市有三所高校,其学生会学习部有“干事”人数分别为,现采用分层抽样的方法从这些“干事”中抽取名进行“大学生学习部活动现状”调查.
(1)求应从这三所高校中分别抽取的“干事”人数;
(2)若从抽取的名干事中随机选两名干事,求选出的名干事来自同一所高校的概率.
(本小题满分14分)四棱锥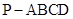 中,
中,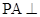 底面
底面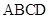 ,
,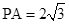 ,
,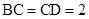 ,
,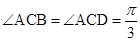 .
.
(1)求证: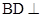 平面
平面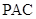 ;
;
(2)若侧棱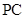 上的点
上的点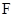 满足
满足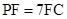 ,求三棱锥
,求三棱锥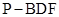 的体积.
的体积.
(本小题满分14分)若抛物线的顶点是双曲线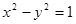 的中心,焦点是双曲线的右顶点.
的中心,焦点是双曲线的右顶点.
(1)求抛物线的标准方程.
(2)若直线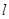 过点
过点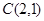 交抛物线于
交抛物线于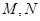 两点,是否存在直线
两点,是否存在直线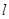 ,使得
,使得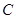 恰为弦
恰为弦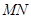 的中点?若存在,
的中点?若存在,
求出直线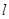 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
(本小题满分12分)某市统计局就某地居民的月收入调查了 10 000 人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1500)).
(Ⅰ)求居民收入在[3 000,3 500)的频率;
(Ⅱ)根据频率分布直方图算出样本数据的中位数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 10 000 人中按分层抽样方法抽出 100 人作进一步分析,则月收入在[2 500,3 000)的这段应抽取多少人?
如图,在多面体 中,四边形
中,四边形 是正方形,
是正方形, .
. .
.
(Ⅰ) 求证: ;
;
(Ⅱ)求二面角 的余弦值的大小.
的余弦值的大小.
已知函数 ,其中
,其中 是
是 的导函数.
的导函数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
如图1,在 中,
中, ,
, 分别是
分别是 上的点,且
上的点,且
 .将
.将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.
(Ⅰ) 是
是 的中点,求
的中点,求 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅱ)求二面角 的正切值.
的正切值.
已知椭圆 上的点
上的点 到左右两焦点
到左右两焦点 的距离之和为
的距离之和为  ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点 的直线
的直线 交椭圆于
交椭圆于 两点.
两点.
(ⅰ)若 轴上一点
轴上一点 满足
满足 ,求直线
,求直线 斜率
斜率 的值;
的值;
(ⅱ)是否存在这样的直线 ,使
,使 的最大值为
的最大值为 (其中
(其中 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线 方
方
程;若不存在,说明理由.
(本小题满分13分)已知椭圆
 (
( )的离心率为
)的离心率为 ,
, 是椭圆的焦点,点
是椭圆的焦点,点 ,直线
,直线 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)设过点 的直线与
的直线与 相交于
相交于 、
、 两点,当
两点,当 的面积最大时,求
的面积最大时,求 的方程.
的方程.
(本小题满分14分)已知函数 在点
在点 处的切线为
处的切线为 .
.
(1)求实数 ,
, 的值;
的值;
(2)是否存在实数 ,当
,当 时,函数
时,函数 的最小值为
的最小值为 ,若存在,求出
,若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若 ,求证:
,求证: .
.