期中备考总动员高三文数学模拟卷【广东】3
有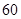 件产品,编号为
件产品,编号为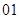 至
至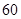 ,现从中抽取
,现从中抽取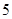 件检验,用系统抽样的方法所确定的抽样编号是
件检验,用系统抽样的方法所确定的抽样编号是
( )
A.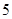 , ,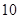 , ,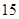 , ,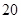 , ,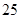 |
B.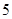 , ,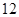 , ,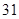 , ,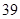 , ,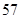 |
C.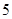 , ,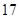 , ,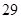 , ,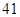 , ,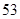 |
D. , ,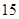 , ,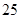 , ,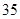 , ,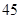 |
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
在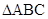 中,
中,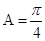 ,
,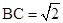 ,则“
,则“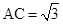 ”是“
”是“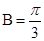 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
已知 ,
, 为两条不同的直线,
为两条不同的直线, ,
, 为两个不同的平面,给出下列
为两个不同的平面,给出下列 个命题:
个命题:
①若 ,
, ,则
,则
②若 ,
, ,则
,则
③若 ,
, ,则
,则
④若 ,
, ,则
,则
其中真命题的序号为( )
| A.①② | B.②③ | C.③④ | D.①④ |
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
(坐标系与参数方程选做题)已知在直角坐标系中,曲线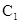 的参数方程为
的参数方程为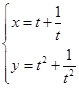 (
( 为
为
参数且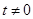 ),在以原点
),在以原点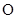 为极点,以
为极点,以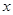 轴正半轴为极轴建立的极坐标系中,曲线
轴正半轴为极轴建立的极坐标系中,曲线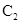 的极坐标方程为
的极坐标方程为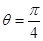 (
( ),则曲线
),则曲线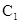 与
与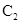 交点的直角坐标为__________.
交点的直角坐标为__________.
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
(本小题满分12分)我市为积极相应《全民健身条例》大力开展学生体育活动,如图是委托
调查机构在市区的两所学校 校、
校、 校中分别随机抽取了
校中分别随机抽取了 名高二年级的学生当月体育锻炼时间的茎
名高二年级的学生当月体育锻炼时间的茎
叶图(单位:小时)

(1)根据茎叶图,分别写将两所学校学生当月体育锻炼 时间的众数、中位数和平均数填入下表;
| |
 校 校 |
 校 校 |
| 众数 |
|
|
| 中位数 |
|
|
| 平均数 |
|
|
(2)根据茎叶图,求 校学生的月体育锻炼时间的方差;
校学生的月体育锻炼时间的方差;
(3)若学生月体育锻炼的时间低于 小时,就说明该生体育锻炼时间严重不足.根据茎叶图估计
小时,就说明该生体育锻炼时间严重不足.根据茎叶图估计 、
、
两所学校的学生体育锻炼严重不足的频率.
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
(本小题满分14分)四棱锥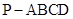 中,
中,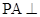 底面
底面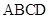 ,
,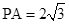 ,
,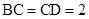 ,
,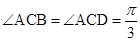 .
.
(1)求证: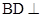 平面
平面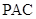 ;
;
(2)若侧棱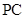 上的点
上的点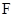 满足
满足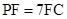 ,求三棱锥
,求三棱锥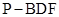 的体积.
的体积.
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
【改编】(本小题满分14分)已知数列 中,
中,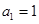 ,且点
,且点 (
(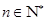 )均在函数
)均在函数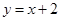 的
的
图象上.
(1)求数列 的通项公式;
的通项公式;
(2)设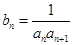 ,求数列
,求数列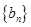 的前
的前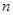 项和
项和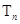 .
.
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
(本小题满分14分)已知椭圆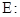
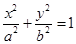 (
(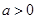 ,
,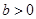 )的离心率
)的离心率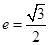 ,并且经过
,并且经过
定点 .
.
(1)求椭圆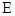 的方程;
的方程;
(2)问是否存在直线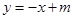 ,使直线与椭圆交于
,使直线与椭圆交于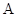 ,
,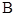 两点,满足
两点,满足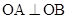 ?若存在,求
?若存在,求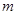 的
的
值;若不存在,说明理由.
来源:2015年期中备考总动员高三文数学模拟卷【广东】3
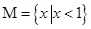 ,
,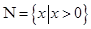 ,则
,则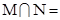 ( )
( )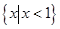
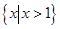
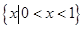
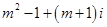 在复平面内对应的点在实轴上,则实数
在复平面内对应的点在实轴上,则实数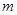 的值是( )
的值是( )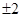
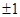
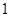
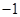
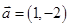 ,
,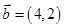 ,则
,则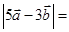 ( )
( )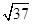
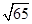
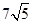
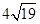
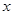 ,
,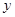 满足
满足 ,则
,则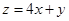 的最大值为( )
的最大值为( )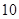
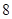
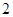

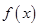 为奇函数,且当
为奇函数,且当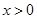 时,
时,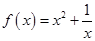 ,则
,则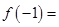 ( )
( )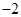
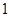
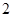
 (
( ,
, )的一条渐近线为
)的一条渐近线为 ,则它的离心率为( )
,则它的离心率为( )



 表示
表示 (
( )的各位数字之和,如
)的各位数字之和,如 ,
, ,
, ,记
,记 ,
, ,
, ,
, ,
, ,则
,则




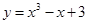 在点
在点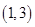 处的切线方程为 .
处的切线方程为 .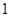 、
、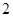 、
、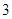 、
、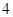 四个数中,任取两个不同的数,其和大于积的概率是________.
四个数中,任取两个不同的数,其和大于积的概率是________.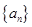 中,若
中,若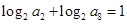 ,则
,则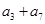 的最小值是 .
的最小值是 . 中,
中,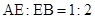 ,若
,若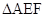 的面
的面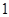
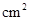 ,则
,则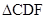 的面积等于________
的面积等于________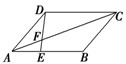
 (
(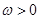 )的最小正周期为
)的最小正周期为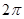 .
.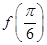 的值;
的值;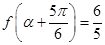 ,
,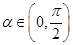 ,求
,求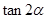 的值.
的值.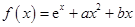 .
.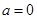 ,
,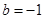 时,求
时,求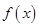 的单调区间;
的单调区间;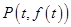
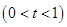 处的切线为
处的切线为 ,直线
,直线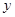 轴相交于点
轴相交于点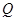 .若点
.若点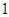 ,求实数
,求实数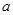 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号