期中备考总动员高三理数学模拟卷【四川】1
将函数 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 ,则
,则 具有性质( )
具有性质( )
A.最大值为 ,图象关于直线 ,图象关于直线 对称 对称 |
B.在 上单调递增,为奇函数 上单调递增,为奇函数 |
C.在 上单调递增,为偶函数 上单调递增,为偶函数 |
D.周期为 ,图象关于点 ,图象关于点 对称 对称 |
已知 ,
, ,且
,且 .现给出如下结论:
.现给出如下结论:
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ ;
;
⑥ .
.
其中正确结论的序号是( )
| A.①③⑤ | B.①④⑥ | C.②④⑥ | D.②③⑤ |
对于实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,设
,设 ,且关于
,且关于 的方程为
的方程为 恰有三个互不相等的实数根
恰有三个互不相等的实数根 ,则
,则 的取值范围是___________.
的取值范围是___________.
对于定义在 上的函数
上的函数 ,若存在距离为
,若存在距离为 的两条直线
的两条直线 和
和 ,使得对任意
,使得对任意 都有
都有 恒成立,则称函数
恒成立,则称函数 有一个宽度为
有一个宽度为 的通道.给出下列函数:
的通道.给出下列函数:
① ;②
;② ;③
;③ ;④
;④
其中在区间 上通道宽度可以为
上通道宽度可以为 的函数有 (写出所有正确的序号).
的函数有 (写出所有正确的序号).
(本小题满分12分)退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”, [60,80]为“老年人”.
(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知四棱锥 ,侧面
,侧面 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 为菱形,且
为菱形,且 .
.
(1)求证: ;
;
(2)求平面 与平面
与平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
(本小题满分14分)已知首项为 ,公比不等于
,公比不等于 的等比数列
的等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
 .
.
(本小题满分13分)已知抛物线 ,圆
,圆 .
.
(1)在抛物线 上取点
上取点 ,
, 的圆周上取一点
的圆周上取一点 ,求
,求 的最小值;
的最小值;
(2)设
 为抛物线
为抛物线 上的动点,过
上的动点,过 作圆
作圆 的两条切线,交抛物线
的两条切线,交抛物线 于
于 、
、 点,求
点,求 中点
中点 的横坐标的取值范围.
的横坐标的取值范围.
 ,则
,则 ( )
( )



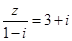 ,i是虚数单位,则复数z的虚部为( )
,i是虚数单位,则复数z的虚部为( )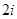
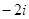


 ,
, ,
,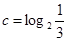 ,则 ( )
,则 ( )
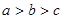


 和平面
和平面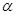 ,则下列命题正确的是( )
,则下列命题正确的是( )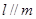 ,
, ,则
,则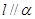
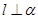 ,
,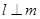
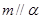
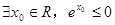
 是
是 的充分条件
的充分条件 ,
,
 的充要条件是
的充要条件是
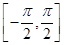 上随机取一个
上随机取一个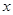 ,
,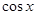 的值介于
的值介于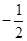 与
与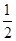 之间的概率为( )
之间的概率为( )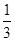
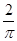






 满足
满足 ,若
,若 则
则 ( )
( ) 值为
值为 ,则
,则 等于______.
等于______.
 满足约束条件
满足约束条件 ,则
,则 的最大值是____________.
的最大值是____________. 上的点,
上的点, 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若 ,则
,则 的面积为______________
的面积为______________ ,
,
 .
. 的周期及单调递减区间;
的周期及单调递减区间; 中,内角
中,内角 所对边的长分别是
所对边的长分别是 ,若
,若 ,求b.
,求b. 在点
在点 处的切线为
处的切线为 .
. ,
, 的值;
的值; ,当
,当 时,函数
时,函数 的最小值为
的最小值为 ,若存在,求出
,若存在,求出 ,求证:
,求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号