高中数学组合几何解答题

（本小题满分14分）已知二次函数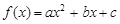满足：①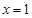时有极值；②图象过点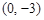，且在该点处的切线斜率为.
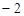（I）求f（x）的解析式；
（II）若曲线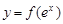上任意一点的切线的斜率恒大于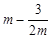，求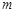的取值范围；
（Ⅲ）当非零实数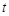满足什么条件时，函数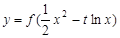的图象与坐标轴没有公共点？

已知函数f (x)=lnx，g(x)=e^x．
（I）若函数φ (x) =" f" (x)－，求函数φ (x)的单调区间；
（Ⅱ）设直线l为函数 y＝f (x) 的图象上一点A(x₀，f (x₀))处的切线．证明：在区间(1，+∞)上存在唯一的x₀，使得直线l与曲线y=g(x)相切．
注：e为自然对数的底数．

已知函数
（1）求该函数的导函数；
（2）求曲线在点处的切线方程．

已知函数.
(Ⅰ)求函数的单调区间；
(Ⅱ)求证：当时，.

已知：函数.（其中e为自然对数的底数，e=2.71828…〉.
(1) 当时，求函数的图象在点处的切线方程；
(2) 当时，试求函数的极值；
(3)若，则当时，函数的图象是否总在不等式所表示的平面区域内，请写出判断过程.

（本小题满分14分）已知函数
（I）若曲线在点处的切线与直线垂直，求a的值；
（II）若在区间单调递增，求a的取值范围；
（III）若—1＜a＜3，证明：对任意都有＞1成立.

（本小题满分14分）
已知 , 函数．
（Ⅰ）求函数的单调区间；
（Ⅱ）若函数的图像在点处的切线的斜率为，问：在什么范围
取值时，对于任意的，函数在区间上总存在
极值？
（Ⅲ）当时，设函数，若在区间上至少存在
一个，使得成立，试求实数的取值范围．

已知函数
（1）求曲线在点处的切线的方程；
（2）直线为曲线的切线，且经过原点，求直线的方程及切点的坐标；
（3）如果曲线的某一切与直线垂直，求切点坐标和切线方程。

(本题满分14分) 已知
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）若在处有极值，求的单调递增区间；
（Ⅲ）是否存在实数，使在区间的最小值是3，若存在，求出的值；
若不存在，说明理由.

（本小题满分14分）已知函数，其中．
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）当时，求的单调区间；
（Ⅲ）证明：对任意的在区间内均存在零点．

已知函数其中常数
（1）当时，求函数的单调递增区间；
（2）当时，给出两类直线：与，其中为常数，判断这两类直线中是否存在的切线，若存在，求出相应的或的值，若不存在，说明理由.
（3）设定义在上的函数在点处的切线方程为，当若在内恒成立，则称为函数的“类对称点”，当时，试问是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标，若不存在，说明理由.

（本题满分14分）已知函数．
（Ⅰ）求函数的单调区间；
（Ⅱ）若函数的图像在点处的切线的倾斜角为，问：在什么范围取值时，对于任意的，函数在区间上总存在极值？
（Ⅲ）当时，设函数，若在区间上至少存在一个，使得成立，试求实数的取值范围．

（本小题14分）已知函数,曲线在处的切线方程为,若时, 有极值.
(1)求的值; (2)求在区间上的最大值和最小值.

（本小题满分13分）已知函数，其中是常数.
（Ⅰ）当时，求在点处的切线方程；
（Ⅱ）求在区间上的最小值.

（本小题满分13分）
已知函数，其中是常数.
(Ⅰ)当时，求曲线在点处的切线方程；
（Ⅱ）若存在实数，使得关于的方程在上有两个不相等的实数根，求的取值范围.