高中数学组合几何解答题

已知曲线f (x ) = ax ² ＋2在x=1处的切线与2x-y+1=0平行.
求由曲线y="f" (x ) 与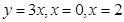所围成的平面图形的面积.

已知函数，．
（Ⅰ）若函数在处取得极值，试求的值，并求在点处的切线方程；
（Ⅱ）设，若函数在上存在单调递增区间，求的取值范围．

已知函数的导数满足，，其中常数，求曲线在点处的切线方程.

已知函数　f(x)＝在[1，＋∞)上为减函数，求实数a的取值范围.

已知函数 (＞0)的图象在点处的切线方程为.
(1)用表示；
(2)若在上恒成立，求的取值范围；
(3)证明：1+++…+＞+.

已知函数f(x)＝x³－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.
(1)求使直线l和y＝f(x)相切且以P为切点的直线方程；
(2)求使直线l和y＝f(x)相切且切点异于P的直线方程．

已知函数在处取得极值，过点作曲线的切线,（1）求此切线的方程.（2）求切线与函数的图象围成的平面图形的面积。

设f(x)=2x³+ax+bx+1  的导数为,若函数的图象关于直线 对称，且.](Ⅰ)求实数,的值;(5分)(Ⅱ)求函数的极值

已知是定义在R上的函数，其图象交轴于A、B、C三点，若B点坐标为，且在和上有相同的单调性，在和上有相反的单调性．
（1）求的值；
（2）在函数的图象上是否存在一点，使得在点M的切线的斜率为？若存在，求出M点的坐标；若不存在，说明理由；
（3）求的取值范围．

已知函数f （x）=lnx，g（x）=e^x．
（I）若函数φ （x） = f （x）－，求函数φ （x）的单调区间；
（Ⅱ）设直线l为函数的图象上一点A（x₀，f （x₀））处的切线．证明：在区间（1，+∞）上存在唯一的x₀，使得直线l与曲线y=g（x）相切．

已知函数
（Ⅰ）若曲线在点处的切线的倾斜角为，求实数的值；
（Ⅱ）若函数在区间上单调递增，求实数实数的范围．

已知函数
(Ⅰ)证明：曲线
（Ⅱ）若,求的取值范围。

设函数，曲线过P（1,0），且在P点处的切斜线率为2．
（I）求a，b的值；
（II）证明：

已知函数在处取得极值.
（1）讨论和是函数的极大值还是极小值；
（2）过点作曲线的切线，求此切线方程.[

已知函数在点的切线方程为
（1）求的值；
（2）当时，的图像与直线有两个不同的交点，求实数的取值范围；
（3）证明对任意的正整数，不等式都成立.