(本小题满分12分)已知函数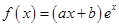 (
(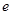 为自然对数的底数),曲线
为自然对数的底数),曲线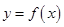 在点
在点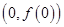 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.
已知函数 .
.
(1)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)当 时,在函数
时,在函数 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为 ,试探究函数
,试探究函数 在Q
在Q 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?
(3)试判断当 时
时 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.
(本小题满分12分) 已知 (
(
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围.
已知函数f(x)=ln x,g(x)= x2-bx(b为常数).
x2-bx(b为常数).
(1)函数f(x)的图像在点(1,f(1))处的切线与g(x)的图像相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数b的取值范围.
已知函数

(1)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数 在
在 =1处取得极值,对任意的
=1处取得极值,对任意的 ∈(0,+∞),
∈(0,+∞), ≥
≥ 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)当 >
> >
> 时,求证:
时,求证:
(本小题12分)已知函数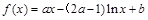 .
.
(Ⅰ)若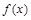 在点(
在点(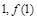 )处的切线方程为
)处的切线方程为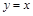 ,求实数
,求实数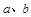 的值;
的值;
(Ⅱ)当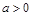 时,讨论
时,讨论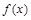 的单调性;
的单调性;
(Ⅲ)当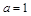 时,
时,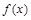 在区间
在区间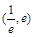 上恰有一个零点,求实数
上恰有一个零点,求实数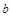 的取值范围.
的取值范围.
(本小题满分12分)
已知函数f(x)=lnx- ,其中a为常数,且a>0.
,其中a为常数,且a>0.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,求函数f(x)的单调递减区间;
(2)若函数f(x)在区间[1,3]上的最小值为 ,求a的值.
,求a的值.
已知函数f(x)=k(x﹣1)ex+x2.
(Ⅰ)当时k=﹣ ,求函数f(x)在点(1,1)处的切线方程;
,求函数f(x)在点(1,1)处的切线方程;
(Ⅱ)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(Ⅲ)当k≤﹣l时,求函数f(x)在[k,1]上的最小值m.
已知函数 R).
R).
(1)若曲线 在点
在点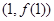 处的切线与直线
处的切线与直线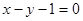 平行,求
平行,求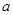 的值;
的值;
(2)在(1)条件下,求函数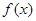 的单调区间和极值;
的单调区间和极值;
(3)当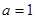 ,且
,且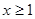 时,证明:
时,证明: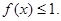
设函数 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且函数
,且函数 为偶函数.若函数
为偶函数.若函数 满足下列条件:
满足下列条件:
① ;
;
②对一切实数 ,不等式
,不等式 恒成立.
恒成立.
(1)求函数 的表达式;
的表达式;
(2)求证:
 .
.
已知函数 ,
, 在点
在点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若在区间 内,恒有
内,恒有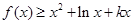 成立,求
成立,求 的取值范围.
的取值范围.