高中数学组合几何解答题

（本小题满分14分）
已知函数．
⑴若，求曲线在点处的切线方程；
⑵若函数在其定义域内为增函数，求正实数的取值范围；
⑶设函数，若在上至少存在一点，使得成立，求实数的取值范围．

（本小题满分10分）求过点P（2，2）且与曲线y=x²相切的直线方程.

（本小题满分12分）
已知函数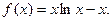
（I）求函数处的切线的方程；
（II）设实数

已知函数．
(Ⅰ)若无极值点，但其导函数有零点，求的值；
(Ⅱ)若有两个极值点，求的取值范围，并证明的极小值小于．

（本小题满分10分）
设函数若曲线的斜率最小的切线与直线平行，求
⑴的值
⑵函数的单调区间
⑶若在上恒成立，求c的取值范围

设函数为奇函数，其图象在点处的切线与直线垂直，导函数的最小值为．
（Ⅰ）求，，的值；
（Ⅱ）求函数的单调递增区间，并求函数在上的最大值和最小值．

16. （本小题满分14分)
两条曲线  都经过点, 并且它们在点处有公共的切线，求，，的值。

设函数.
（1） 求的单调区间与极值；
（2）是否存在实数，使得对任意的，当时恒有成立．若存在，求的范围，若不存在，请说明理由．

证明：若函数在点处可导，则函数在点处连续．

已知函数f(x)=，其中a>0.
（Ⅰ）若a=1，求曲线y=f(x)在点（2，f(2)）处的切线方程；
（Ⅱ）若在区间上，f(x)>0恒成立，求a的取值范围.

已知曲线与在处的切线互相垂直,求的值.

曲线在点处的切线与x轴交点的横坐标为a_n．
（1）求a_n；
（2）设，求数到的前n项和S_n．

已知函数．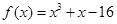
（1）求曲线在点处的切线方程；
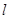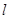（2）直线为曲线的切线，且经过原点，求直线的方程及切点坐标．

已知函数f(x)=x－ax+(a－1)，。
（1）讨论函数的单调性；       
（2）证明：若，则对任意x，x，xx，有。

(本小题满分l2分)求垂直于直线并且与曲线相切的直线方程.