江苏省丰县修远双语学校第一学期第三次月考高二数学
设椭圆C1的离心率为 ,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。
,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为 _____________。
若将一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),先后抛掷两次,则出现向上的点数之和为4的概率是 ___________________.
在平面直角坐标系 中,设
中,设 是横坐标与纵坐标的绝对值均不大于2的点构成的区域,
是横坐标与纵坐标的绝对值均不大于2的点构成的区域, 是到原点的距离不大于1的点构成的区域,向
是到原点的距离不大于1的点构成的区域,向 中随机投一点,则所投点在
中随机投一点,则所投点在 中的概率是 _______________________
中的概率是 _______________________
.某校共有学生2000名,各年级男、女生人数如表1.已知在全校学生中随机抽取1名,
抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为___________
| |
一年级 |
二年级 |
三年级 |
| 女生 |
373 |
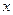 |
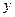 |
| 男生 |
377 |
370 |
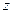 |
表1

某地区为了解70 80岁的老人的日平均睡眠时间(单位:
80岁的老人的日平均睡眠时间(单位: ),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号 |
分组 (睡眠时间) |
组中值( ) ) |
频数 (人数) |
频率( ) ) |
| 1 |
 |
 |
6 |
 |
| 2 |
 |
 |
10 |
 |
| 3 |
 |
 |
20 |
 |
| 4 |
 |
 |
10 |
 |
| 5 |
 |
 |
4 |
 |
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为 ______________________________
(本小题满分14分)
袋子中有红、白、黄、黑、颜色不同大小相同的四个小球。
(1)从中任取一球,求取出白球的概率。
(2)从中任取两球,求取出的是红球、白球的概率。
(3)从中先后各取一球,求先后取出的分别是红球、白球的概率。

(本小题满分15分)
设 ,椭圆方程为
,椭圆方程为 ,抛物线方程为
,抛物线方程为 .如图4所示,过点
.如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为 ,已知抛物线在点
,已知抛物线在点 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
(本小题满分15分)
(文)已知直线 与曲线
与曲线 相切,分别求
相切,分别求 的方程,使之满足:
的方程,使之满足:
(1) 经过点
经过点 ;(2)
;(2) 经过点
经过点 ;(3)
;(3) 平行于直线
平行于直线 ;
;
(理)如图,平面 平面
平面 ,四边形
,四边形 与
与 都是直角梯形,
都是直角梯形,


 ,
,

 ,
, 分别为
分别为 的中点
的中点
(Ⅰ)证明:四边形 是平行四边形;
是平行四边形;
(Ⅱ) 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设 ,证明:平面
,证明:平面 平面
平面 ;
;
 经过抛物线
经过抛物线 的焦点,则实数
的焦点,则实数 ______________ .
______________ .
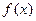 的图象是折线段
的图象是折线段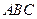 ,其中
,其中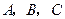
 ,则
,则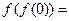 ;
;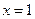 处的导数
处的导数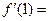 .
. 、
、 、
、 、
、 、
、
 是幂函数,则函数
是幂函数,则函数 "的否定是____________________________________.
"的否定是____________________________________. 是曲线
是曲线 的一条切线,则实数的
的一条切线,则实数的 值是 ________________.
值是 ________________. 是抛物线
是抛物线 的焦点,过
的焦点,过 于
于 两点.设
两点.设 ,则
,则 与
与 的比值等于 .
的比值等于 . 中,椭圆
中,椭圆 的焦距为2c,以O为圆心,
的焦距为2c,以O为圆心, 为半径作圆
为半径作圆 ,若过
,若过 作圆
作圆
 都经过点
都经过点 , 并且它们在点
, 并且它们在点 处有公共的切线,求
处有公共的切线,求 ,
, ,
, 的值。
的值。 的焦点为点
的焦点为点 ,
, ,点
,点 为椭圆上的一动点,当
为椭圆上的一动点,当 为钝角时,求点
为钝角时,求点 =1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2:
=1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
. ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若 ,求直线l的方程.
,求直线l的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号