(本小题满分15分)
(文)已知直线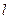 与曲线
与曲线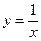 相切,分别求
相切,分别求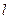 的方程,使之满足:
的方程,使之满足:
(1)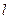 经过点
经过点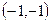 ;(2)
;(2)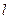 经过点
经过点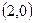 ;(3)
;(3)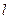 平行于直线
平行于直线 ;
;
(理)如图,平面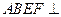 平面
平面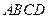 ,四边形
,四边形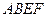 与
与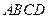 都是直角梯形,
都是直角梯形,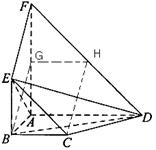
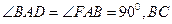

 ,
,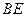

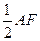 ,
, 分别为
分别为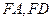 的中点
的中点
(Ⅰ)证明:四边形 是平行四边形;
是平行四边形;
(Ⅱ) 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设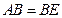 ,证明:平面
,证明:平面 平面
平面 ;
;
推荐套卷
(本小题满分15分)
(文)已知直线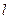 与曲线
与曲线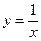 相切,分别求
相切,分别求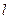 的方程,使之满足:
的方程,使之满足:
(1)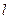 经过点
经过点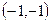 ;(2)
;(2)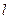 经过点
经过点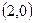 ;(3)
;(3)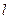 平行于直线
平行于直线 ;
;
(理)如图,平面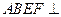 平面
平面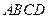 ,四边形
,四边形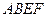 与
与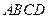 都是直角梯形,
都是直角梯形,
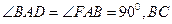

 ,
,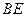

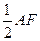 ,
, 分别为
分别为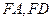 的中点
的中点
(Ⅰ)证明:四边形 是平行四边形;
是平行四边形;
(Ⅱ) 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设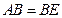 ,证明:平面
,证明:平面 平面
平面 ;
;