高中数学表面展开图填空题

已知矩形的周长为，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为        ．

一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动，则该小球表面永远不可能接触到的容器内壁的面积是         ．

一个几何体的三视图如图所示，则该几何体的体积为  

若两个球的表面积之比为，则这两个球的体积之比为          ．

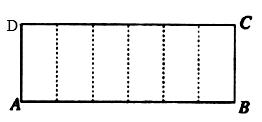
如图所示，在确定的四面体中，截面平行于对棱和.

(1)若⊥，则截面与侧面垂直；
(2)当截面四边形面积取得最大值时，为中点；
(3)截面四边形的周长有最小值；
(4)若⊥，，则在四面体内存在一点到四面体六条棱的中点的距离相等.上述说法正确的是            ．

已知正四棱锥O－ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为________．

已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为的正方形．若，则△OAB的面积为_______．

已知直三棱柱中，，侧面的面积为，则直三棱柱外接球表面积的最小值为         ．

已知直三棱柱中，，侧面的面积为，则直三棱柱
外接球表面积的最小值为         ．

某几何体的三视图如右图,则此几何体的体积为        ．

已知矩形的周长为，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为        ．

一个几何体的三视图如图所示，则这个几何体的体积为          ．

如图，在棱柱的侧棱上各有一个动点，且满足，是棱上的动点，则的最大值是          ．

利用一个球体毛坯切削后得到一个四棱锥,其中底面四边形是边长为的正方形，，且平面,则球体毛坯体积的最小值应为       ．

已知的三边长分别为，，，是边上的点，是平面外一点．给出下列四个命题：
①若平面，且是边中点，则有；
②若，平面，则面积的最小值为；
③若，平面，则三棱锥的外接球体积为；
④若，在平面上的射影是内切圆的圆心，则三棱锥的体积为；
其中正确命题的序号是            （把你认为正确命题的序号都填上）．