(本小题满分14分) 如图,在四棱锥 中,底面
中,底面 为矩形,平面
为矩形,平面 平面
平面 ,
, ,
, ,
, 为
为 的中点,求证:
的中点,求证:
(Ⅰ) 平面
平面 ;
;
(Ⅱ)平面 平面
平面 ;
;
(Ⅲ)求四棱锥 的体积.
的体积.
(本小题满分12分)在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=1,AB=4,BC=2 ,∠CBA=30°.
,∠CBA=30°.
(1)求证:AC⊥PB;
(2)当PD=2时,求此四棱锥的体积.
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积 的大小;
的大小;
(Ⅱ)求异面直线DE与AB所成角的余弦值;
(Ⅲ)求二面角A-ED-B的正弦值.
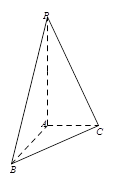
(本小题满分12分)如图,在三棱锥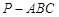 中,
中, 丄平面
丄平面 ,
,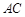 丄
丄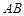 ,
, ,
, .
.
(Ⅰ)证明: 丄
丄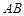 ;
;
(Ⅱ)求二面角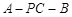 的正弦值;
的正弦值;
(Ⅲ)求三棱锥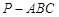 外接球的体积.
外接球的体积.
(本题14分)一个圆锥的底面半径为 ,高为
,高为 ,其中有一个高为
,其中有一个高为 的内接圆柱:
的内接圆柱:
(1)求圆锥的侧面积;
(2)当 为何值时,圆柱侧面积最大?并求出最大值.
为何值时,圆柱侧面积最大?并求出最大值.
如图所示, 是正方形,
是正方形, ,
, 是
是 的中点
的中点 
(1)求证: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,
, ,
, 为
为 的中点,
的中点, 为
为 上一点,且
上一点,且 .
.
(1)证明: 平面
平面 ;
;
(2)证明: 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
在长方体 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(1)求棱 的长;
的长;
(2)求经过 四点的球的表面积.
四点的球的表面积.
(本题12分)如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC= ,动点D在线段AB上.
,动点D在线段AB上.
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
(本题12分)如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求四棱锥P—ABCD的表面积S.
(本小题满分10分)如图,已知△ 是边长为4的正三角形,
是边长为4的正三角形, 是
是 的中点,
的中点, ,
, 分别是边
分别是边 ,
, 上的点,且
上的点,且 ,设
,设 .
.
(Ⅰ)试将线段 的长表示为
的长表示为 的函数;
的函数;
(Ⅱ)设△ 的面积为
的面积为 ,求
,求 的解析式,并求
的解析式,并求 的最小值;
的最小值;
(Ⅲ)若将折线 绕直线
绕直线 旋转一周得到空间几何体,试问:该几何体的体积是否有最小值?若有,求出它的最小值;若没有,请说明理由.
旋转一周得到空间几何体,试问:该几何体的体积是否有最小值?若有,求出它的最小值;若没有,请说明理由.
(本小题满分12分)在长方体 中,
中, ,过
,过 ,
, ,
, 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,这个几何体的体积为
,这个几何体的体积为 。
。
(1)求棱 的长;
的长;
(2)求经过 ,
, ,
, ,
, 四点的球的表面积。
四点的球的表面积。