（本题12分）如图，在三棱锥A－BOC中，OA⊥底面BOC，∠OAB＝∠OAC＝30°，AB＝AC＝4，BC＝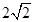
，动点D在线段AB上．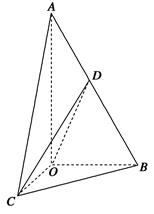
（1）求证：平面COD⊥平面AOB；
（2）当OD⊥AB时，求三棱锥C－OBD的体积．
中，已知
,
是
边上的一点，
，求
的长.
的面积是
，内角
所对边长分别为
，
。
.
，求
的值
的一元二次不等式
对于一切实数
，求证：
不可能都是奇数。
若非
是
的
充分不必要条件，求
的取值范围。相关知识点
推荐套卷
（本题12分）如图，在三棱锥A－BOC中，OA⊥底面BOC，∠OAB＝∠OAC＝30°，AB＝AC＝4，BC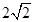＝，动点D在线段AB上．
（1）求证：平面COD⊥平面AOB；
（2）当OD⊥AB时，求三棱锥C－OBD的体积．
粤公网安备 44130202000953号