高中数学表面展开图解答题

（本小题满分12分）如图1所示，直角梯形，，，，、为线段、上的点，且，设，沿将梯形翻折，使平面平面（如图2所示）．

（1）若以、、、为顶点的三棱锥体积记为，求的最大值及取最大值时的位置；
（2）在（1）的条件下，试在线段上的确定一点使得，并求直线与平面所成的角的正弦值．

在如图所示的几何体中，四边形ABCD是正方形，MA⊥平面ABCD，PD∥MA，E、G、F分别为MB、PB、PC的中点，且AD＝PD＝2MA．

（1）求证：平面EFG∥平面PMA；
（2）求证：平面EFG⊥平面PDC；
（3）求三棱锥P－MAB与四棱锥P－ABCD的体积之比．

如图，四边形ABCD为矩形，四边形ADEF为梯形，FEAD，∠AFE=60°，且平面ABCD⊥平面ADEF，AF=FE=AB=2，点G为AC的中点．

（Ⅰ）求证：EG∥平面ABF；
（Ⅱ）求三棱锥B﹣AEG的体积．

如图，已知三棱锥中，,，且⊥，⊥，且在平面上的射影恰好在上．

（1）求证：⊥；
（2）求证：平面⊥平面；
（3）求三棱锥的体积．

（本小题满分14分）
如图，在多面体中，平面，∥，平面平面，，，．

（1）求证：∥；
（2）求三棱锥的体积．

已知三棱柱ABC－A′B′C′中，平面BCC′B′⊥底面ABC，BB′⊥AC，底面ABC是边长为2的等边三角形，AA′＝3，E、F分别在棱AA′，CC′上，且AE＝C′F＝2．

（1） 求证：BB′⊥底面ABC；
（2）在棱A′B′上是否存在一点M，使得C′M∥平面BEF，若存在，求值，若不存在，说明理由
（3）求棱锥-BEF的体积

如图，在两块钢板上打孔，用钉帽呈半球形、钉身为圆柱形的铆钉（图1）穿在一起，在没有帽的一端锤打出一个帽，使得与钉帽的大小相等，铆合的两块钢板，成为某种钢结构的配件，其截面图如图2.（单位：mm）（加工中不计损失）.

（1）若钉身长度是钉帽高度的2倍，求铆钉的表面积；
（2）若每块钢板的厚度为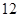mm，求钉身的长度（结果精确到mm）.

（本小题满分12分）如图（1），在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图所示（2）.

（Ⅰ）求证:平面；
（Ⅱ）求几何体的体积.

如图，四边形为菱形，，平面，为中点．

（Ⅰ）求证：平面平面；
（Ⅱ）若，求三棱锥的体积．

如图，在直三棱柱ABC­A₁B₁C₁中，AB＝AC＝5，BB₁＝BC＝6，D，E分别是AA₁和B₁C的中点．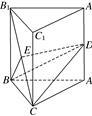

（1）求证：DE∥平面ABC；
（2）求三棱锥E­BCD的体积．

如图，在四棱锥中，平面平面，∥是正三角形，已知

（1）设是上的一点，求证:平面平面；
（2）求四棱锥的体积．

如图，在直三棱柱中，底面是正三角形，点是中点，，．

（Ⅰ）求三棱锥的体积；
（Ⅱ）证明：．

如图，在四棱锥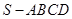中，底面ABCD是菱形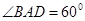，，侧面底面ABCD，并且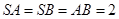，F为SD的中点.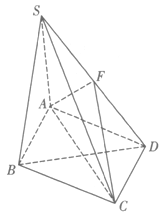

（1）求三棱锥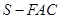的体积；
（2）求直线BD与平面FAC所成角的正弦值.

（本小题满分12分）如图，矩形中，对角线的交点为⊥平面为上的点，且．
（I）求证：⊥平面；
（II）求三棱锥的体积．

（本小题12分）第（1）小题5分，第（2）题7分
如图，在四棱锥中中，底面为菱形，，，点在线段上，且，为的中点．

（1）求证：平面；
（2）若平面平面，求三棱锥的体积；